Cho hàm số y = x - 3 có đồ thị (d) và hàm số y = - 1/2x + 2 có đồ thị (D).
b) Xác định các hệ số a và b của hàm số y= ax +b(a khác 0) biết rằng đồ thị (d') của hàm số này song song với (d) và cắt (D) tại điểm có tung độ bằng 2.
Những câu hỏi liên quan
Cho hàm số y=-2x+1 (d)
a) Vẽ đồ thị (d) của hàm số y=-2x+1
b) Xác định các hệ số a và b của hàm số y=ax+b, biết rằng đồ thị của hàm số này song song với đồ thị (d) và đi qua điểm A(2;1).
b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: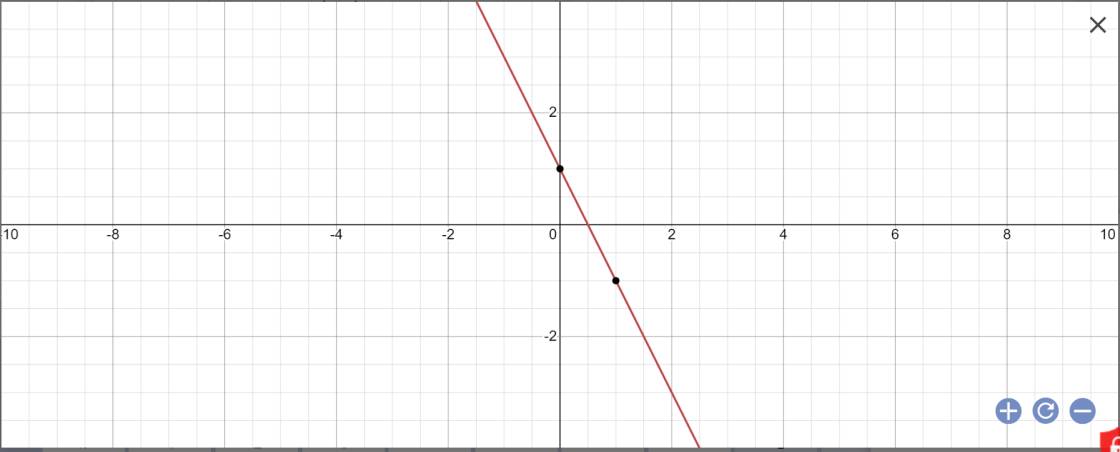 
Đúng 1
Bình luận (0)
Vẽ đồ thị (d) của hàm số y=2x–6 (1đ) 2) Xác định các hệ số a và b của hàm số y = ax + b, biết rằng đồ thị ( d”) của hàm số này song song với (d) và cắt trục hoành tại điểm có hoành độ bằng 5,
Vì (d'')//(d) nên a=2
=>y=2x+b
Thay x=5 và y=0 vào (d''), ta được:
b+10=0
=>b=-10
Đúng 0
Bình luận (0)
a,Vẽ (d) của hàm số y=2x+5
b,Xác định các hệ số a và b của hàm số y=ax+b, biết rằng đồ thị (d') của hàm số này song song với (d) và cắt trục hoành tại điểm có hoành độ bằng 3
a)
\(x=0\Rightarrow y=5\)
\(\Rightarrow A\left(0;5\right)\)
\(x=-1\Rightarrow y=3\)
\(\Rightarrow B\left(0;3\right)\)
b) Ta có (d') // (d)
\(\Rightarrow\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a'=2\\b\ne5\end{matrix}\right.\)
\(\Rightarrow\left(d'\right):y=2x+b\)
(d') cắt trục hoành tại điểm có hoành độ (3;0), suy ra
\(0=2.3+b\)
\(\Leftrightarrow b=6\)
vậy a = 2; b = 6
Đúng 0
Bình luận (0)
vẽ đồ thị (d) của hàm số y=2x-5
xác định các hệ số a và b của hàm số y=ax+b biết rằng đồ thị (dC) của hàm ssố này song song với (d) và cắt trục hoành tại điểm có hoành độ bằng 5
Bài 2: Cho hàm số y=2x-6 có đồ thị là đường thẳng (d)
a) Vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy
b) Xác định các hệ số a, b của hàm số y=ax+b biết rằng đồ thị (d') của hàm số này song song với (d) và đi qua điểm I (1; 4)
giải chi tiết cụ thể giúp mk vớiiiiiiiiii ạh
b: Vì (d')//(d) nên a=2
Vậy: (d'): y=2x+b
Thay x=1 và y=4 vào (d'), ta được:
b+2=4
hay b=2
Đúng 1
Bình luận (1)
cho hàm số y = -0,5x có đồ thị là (d1) và hàm số y = x + 2 có đồ thị là (d2)
a, vẽ đồ thị (d1) và (d2) trên cùng mặt phẳng toạ độ Oxy
b, xác định hệ số a, b của đường thẳng (d) : y = ax + b biết rằng (d) song song với (d1) và d cắt (d2) tại một điểm có tung độ bằng -3
cho hàm số y = -0,5x có đồ thị là (d1) và hàm số y = x + 2 có đồ thị là (d2)
a, vẽ đồ thị (d1) và (d2) trên cùng mặt phẳng toạ độ Oxy
b, xác định hệ số a, b của đường thẳng (d) : y = ax + b biết rằng (d) song song với (d1) và d cắt (d2) tại một điểm có tung độ bằng -3
cho hàm số y=2x-4
a)vẽ đồ thị (d) của hàm số y=2x-4
b) tính khoảng cách từ gốc tọa độ O đến đường thẳng (d) đơn vị trên trục tọa độ là cm
c)Xác định các hệ số a và b của hàm số y=ax+b, biết rằng đồ thị (d') của hàm số này song song với (d) đi qua điểm A (0;3)
\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho hàm số y=1/2x có đồ thị là (d1),và hàm số y=-2x+5 có đồ thị là (d2).
a)vẽ (d1) và(d2) trên cùng một hệ trục tọa độ
b)tìm tọa độ giao điểm A của (d1) và (d2) bằng phép tính
c)xác định các hệ số a và b của hàm số y=ax+b có đồ thị là đường thẳng (d),biết (d) song song với (d1) và (d) cắt (d2) tại B có tung độ là -3.
1) Vẽ đồ thị (d) của hàm số y = 2x – 3
2) Tìm tọa độ giao điểm của (d) và (d1) y = - 3x + 2 bằng phép tính.
3) Xác định các hệ số a và b của hàm số y = ax + b, biết rằng đồ thị (d2) của hàm số
này cắt trục tung tại điểm có tung độ là -2 và (d), (d1), (d2) đồng quy.
2: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-3=-3x+2\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)