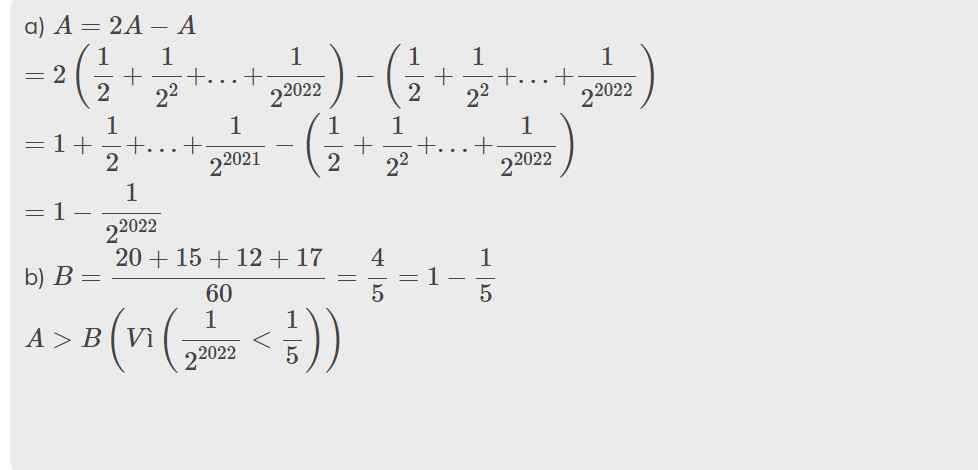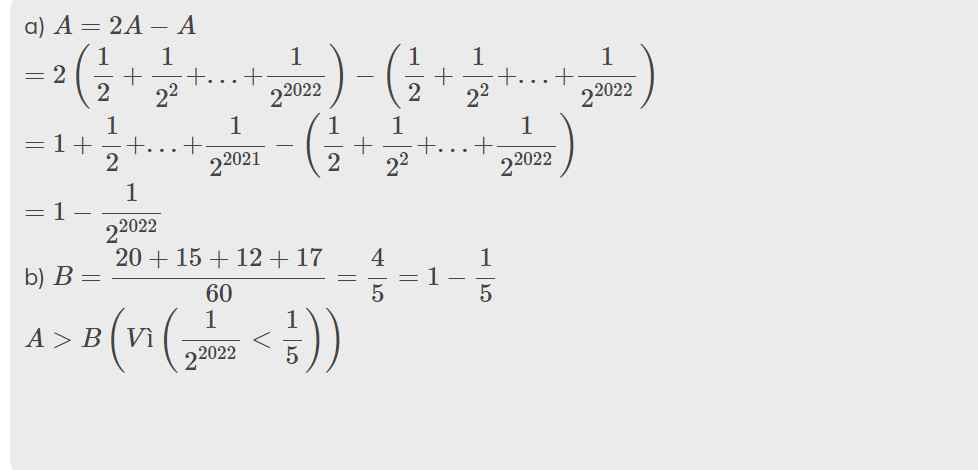Cho A=(1/22-1)(1/32-1)...(1/20132-1)(1/20142-1) và B=-1/2
So sánh A và B

Những câu hỏi liên quan
Tính
C
1
2
–
2
2
+
3
2
–
4
2
+
5
2
–
6
2
+
…
.
+
2013
2
–
2014
2
+
2015
2
Đọc tiếp
Tính C = 1 2 – 2 2 + 3 2 – 4 2 + 5 2 – 6 2 + … . + 2013 2 – 2014 2 + 2015 2
C=12-22+32-42+52-62+..+20132-20142+20152
SSH:(20152-12):10+1=2015
(12-22)+(32-42)+(52-62)+...+(20132-20142)+20152
-10+(-10)+(-10)+...+(-10)+20152
-10x(2015-1):2+20152=12
=> C=12
So sánh :
a) A = 2005.2001 và B = 20062
b) B = (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1) và B = 232
c) C = (3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1) và B = 332 - 1
a) Ta có : 2005.2007 = (2006 - 1)(2006 + 1) = 20062 - 12 = 20062 - 1 ( cái khúc này sửa : 2005.2001 thành 2005.2007)
Mà B = 20062
=> 20062 - 1 < 20062
=> A < B
b) Ta có : B = (2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
B = (2 - 1)(2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
B = (22 - 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
B = (24 - 1)(24 + 1)(28 + 1)(216 + 1)
B = (28 - 1)(28 + 1)(216 + 1) = (216 - 1)(216 + 1) = 232 - 1
Mà C = 232
=> B < C
c) Tương tự như câu b
Câu 1: Thực hiện phép tính.
a) (x4 - 2x3 - 4x2 + 8x) : ( x2 - 4 )
b) 20142 + 142 - 28 . 2014.
Câu 2 : SO SÁNH CẶP SỐ SAU:
A= 2015 . 2013 . ( 20142 + 1 ) và B= 20144
mọi người làm hộ mình với ạ. Mình cảm ơn nhìu nhìu <3
\(1,\\ a,=\left[x^3\left(x-2\right)-4x\left(x-2\right)\right]:\left(x^2-4\right)\\ =x\left(x^2-4\right)\left(x-2\right):\left(x^2-4\right)=x\left(x-2\right)\\ b,=\left(2014-14\right)^2=2000^2=4000000\\ 2,\\ A=2015\cdot2013\cdot\left(2014^2+1\right)\\ A=\left(2014^2-1\right)\left(2014^2+1\right)\\ A=2014^4-1< B=2014^4\)
Đúng 1
Bình luận (0)
bài 1:cho S = 1+2+22+23+...+22023
a. tính tổng
b.cho B = 22024 so sánh S và B
bài 2: tính tổng H=3+32+33+...+32022
Bài 1
a) S = 1 + 2 + 2² + 2³ + ... + 2²⁰²³
2S = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰²⁴
S = 2S - S = (2 + 2² + 2³ + ... + 2²⁰²⁴) - (1 + 2 + 2² + 2³)
= 2²⁰²⁴ - 1
b) B = 2²⁰²⁴
B - 1 = 2²⁰²⁴ - 1 = S
B = S + 1
Vậy B > S
Đúng 2
Bình luận (0)
a,
\(S=1+2+2^2+...+2^{2023}\)
\(2S=2+2^2+2^3+...+2^{2024}\)
\(\Rightarrow S=2^{2024}-1\)
b.
Do \(2^{2024}-1< 2^{2024}\)
\(\Rightarrow S< B\)
2.
\(H=3+3^2+...+3^{2022}\)
\(\Rightarrow3H=3^2+3^3+...+3^{2023}\)
\(\Rightarrow3H-H=3^{2023}-3\)
\(\Rightarrow2H=3^{2023}-3\)
\(\Rightarrow H=\dfrac{3^{2023}-3}{2}\)
Đúng 3
Bình luận (0)
Bài 2
H = 3 + 3² + 3³ + ... + 3²⁰²²
⇒ 3H = 3² + 3³ + 3⁴ + ... + 3²⁰²³
⇒2H = 3H - H
= (3² + 3³ + 3⁴ + ... + 3²⁰²³) - (3 + 3² + 3³ + ... + 3²⁰²²)
= 3²⁰²³ - 3
⇒ H = (3²⁰²³ - 3) : 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hình thang ABCD (AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự ở M và N. a, Chứng minh rằng OM ON. b, Chứng minh rằng frac{1}{AB}+frac{1}{CD}frac{2}{MN}c, Biết SAOB 20132 (đơn vị diện tích); SCOD 20142 (đơn vị diện tích). Tính SABCD.
Đọc tiếp
Hình thang ABCD (AB // CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự ở M và N.
a, Chứng minh rằng OM = ON.
b, Chứng minh rằng \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c, Biết SAOB= 20132 (đơn vị diện tích); SCOD= 20142 (đơn vị diện tích). Tính SABCD.
Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
Bạn xem cách làm tại đây nhé!
So sánh A và B biết :
A= 39/40 và B= 1/ 21 + 1/ 22 + 1/ 23 +.................+ 1/ 79 + 1/ 80
A = 1/2 + 1/22 + 1/23 + 1/24+...+ 1/22021 + 1/22022
và B = 1/3+1/4+1/5+17/60
Hỏi :
a) Rút gọn A
b)So sánh A và B
So sánh A và B biết: A=(2+1)×(2^2+1)×(2^4+1)×(2^8+1)×(2^16+1)×(2^16+1) và B=2^32
Ta có: \(A=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1< 2^{32}\)
\(\Leftrightarrow A< B\)
Đúng 0
Bình luận (0)
Cho A=3(1+4+4 mũ 2 +...+ 4 mũ 39) +1 và B= 32 mũ 15 . So sánh A và B
\(32^{15}=\left(2^5\right)^{15}=2^{5.15}=2^{75}\)
\(4^{39}=\left(2^2\right)^{39}=2^{2.39}=2^{78}\)
Do \(2^{78}>2^{75}\)
\(\Rightarrow4^{39}>32^{15}\)
\(\Rightarrow1+4+4^2+...+4^{39}>32^{15}\)
\(\Rightarrow3\left(1+4+4^2+...+4^{39}\right)>32^{15}\)
Vậy \(A>B\)
Đúng 1
Bình luận (0)