Cho đường tròn O tiếp xúc với hai cạnh MX My của góc xMy tại A và B từ A Vẽ tia song song với MB cắt đường tròn O tại C đoạn MC cắt đường tròn O tại E hai đường thẳng AE MB cắt nhau tại K Chứng minh K là trung điểm của MB

cho góc xMy < VẼ  90, trên tia Mx lấy điểm A, vẽ đường tròn tâm O bất kỳ tiếp xúc với Mx tại A và cắt tia My tại B và C( B nằm giữa M,C). Gọi D là diểm chính giữa cung BC không chứa A. c/m đường thảng AD cố định không phụ thuộc vào vị trí đường tròn tâm O

b, gọi H  là 1 điểm trên đoạn OM sao cho HM/HỒ=(ẦM/ÀO)^2, C/m 4 điểm B,H,O,C nằm trên 1 đường tròn

 cho góc xMy và đường tròn (O) tiếp xúc với Mx và My tại A,B. Qua A vẽ đường thẳng song song với My cắt (O) tại điểm thứ 2 C,đoạn MC cắt (O) tại điểm thứ 2 D, tia AD cắt My tại K, chứng minh: K là trung điểm của MB
trình bày ra

cho tam giác ABC có 3 góc nhọn nội tiếp trong đường tròn (O) (AB<AC). Dường tròn tâm O1 tiếp xúc trong với dường tròn (O) tại M, tiếp xúc với 2 cạnh AB, AC lần lượt tại L,K. Gọi E là giao điểm thứ hai của Mk với (O)
a/ c/m ME là tia phân giác góc AMC
b/tia phân giác Mx của góc BMC cắt LK tại I. CM rằng tứ giác MIKC nội tiếp

Cho nửa đường tròn tâm O đường kính AB=2R (R>9). Trên bán kính OA lấy hai điểm C và D sao cho AC=6; AD=9. Đường thẳng vuông góc với AB tại D cắt nửa đường tròn tại E. Điểm F thuộc nửa đường tròn sao cho  góc ACF=góc DCE. Đường tròn tâm I bán kính r tiếp xúc với 2 cạnh của góc ECF và tiếp xúc trong với đường tròn tâm O. Tính r.

Cho tam giác ABC cân tại A có M là trung điểm của cạnh đáy BC. Trên nửa mặt phẳng bờ BC chứa điểm A ,vẽ \(\widehat{xMy}=\widehat{ABC}\). Tia Mx cắt AB tại D; tia My cắt AC tại E. Chứng minh rằng DE luôn tiếp xúc với 1 đường tròn cố định khi \(\widehat{xMy}\)quay quanh điểm M ?

Giúp mình với!!!

Cho nửa đường tròn tâm O đường kính AB=2R (R>9). Trên bán kính OA lấy hai điểm C và D sao cho AC=6; AD=9. Đường thẳng vuông góc với AB tại D cắt nửa đường tròn tại E. Điểm F thuộc nửa đường tròn sao cho ^ACF=^DCE. Đường tròn tâm I bán kính r tiếp xúc với 2 cạnh của góc ECF và tiếp xúc trong với đường tròn tâm O. Tính r.

Cho nửa đường tròn tâm O đường kính AB=2R (R>9). Trên bán kính OA lấy hai điểm C và D sao cho AC=6; AD=9. Đường thẳng vuông góc với AB tại D cắt nửa đường tròn tại E. Điểm F thuộc nửa đường tròn sao cho \(\widehat{ACF}=\widehat{DCE}\). Đường tròn tâm I bán kính r tiếp xúc với 2 cạnh của góc ECF và tiếp xúc trong với đường tròn tâm O. Tính r.

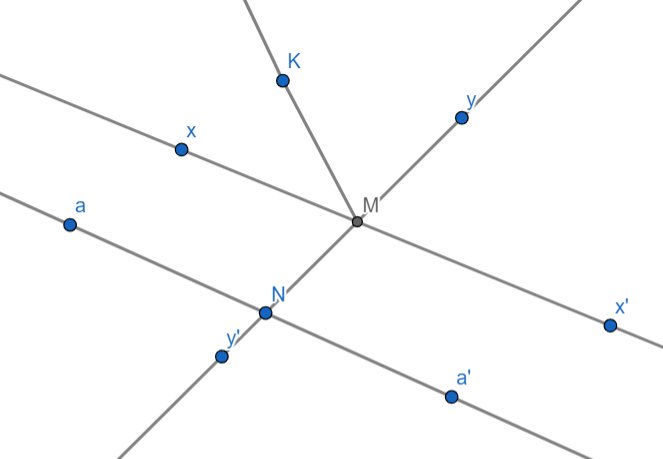
câu 24: vẽ hai đường thẳng xx' và yy' cắt nhau tại M sao cho góc xMy là góc tù . Trên tia My' lấy một điểm N khác M rồi vẽ đường thẳng aa' đi qua N và song song với xx'

a) kể tên các goc có dỉnh N , khoog kể các góc bẹt 

b) lấy điểm K nằm trong góc xMy vẽ tia MK . nêu tên các góc có đỉnh M