Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Đường thẳng AB có tiếp xúc với đường tròn (C; 4 cm) hay không? Vì sao?

Những câu hỏi liên quan
Cho tam giác ABC có AB = 15 cm và AC= 8 cm và BC = 17 cm a) Chứng minh tam giác ABC vuôngb) Gọi AH là đường cao trong tam giác ABC, đường thẳng qua H vuông góc với AB cắt đường tròn (A;AH) tại D. Chứng minh BD là tiếp tuyến của đường tròn (A;AH)c) Tính HD.
Cho tam giác ABC vuông góc tại A. Khẳng định nào sau đây là đúng:
A. Đường tròn (A;AC) tiếp xúc với đường thẳng AB.
B. Đường tròn (C;AB) tiếp xúc với đường thẳng BC.
C. Đường tròn (B;BC) tiếp xúc với đường thẳng AC.
D. Đường tròn (A;BC) cắt đường thẳng BC.
Cho tam giác ABC nội tiếp đường tròn (O). Đường phân giác AD của tam giác ABC cắt cung BC ở E. Đường tròn (I) tiếp xúc trong với (O) và tiếp xúc với BC tại T cắt AD ở M, N (N nằm giữa A và M); CM cắt đường tròn (O) tại K. Vẽ dây KL//AB. Chứng minh rằng ba điểm C, N, L thẳng hàng.
CM được S,T,E thẳng hàng
Xét tam giác ECT zà tam giác EST có \(\widehat{CET}\left(chung\right),\widehat{ECT}=\widehat{ESC}\)
=>tam giác ECT=tam giác EST(g.g)
=>\(\frac{EC}{ES}=\frac{ET}{EC}=>ET.ES=EC^2\)
xét tam giác EMT zà tam giác ESN có \(\widehat{MET}\left(chung\right),\widehat{EMT}=\widehat{ESN}\)
=> tam giác ECT = tam giác ESN(g.g)
=>\(\frac{EM}{ES}=\frac{ET}{EN}=>ET.ES=EM.EN=EM.EN\\\)
Nên \(EC^2=EM.EN=\left(=ET.ES\right)=\frac{EC}{EN}=\frac{EM}{EC}\)
tam giác ECM = tam giasc ENC (c.g.c)
=>\(\widehat{EMC}=\widehat{ENC}\)
=>\(\widehat{ECD}+\widehat{DCM}=\widehat{NAC}+\widehat{NCA}\)
mà \(\widehat{ECD=\widehat{NAC}}\)
nên \(\widehat{DCM}=\widehat{NCA}\)
ta có \(KL//AB=>\widebat{BK}=\widebat{AL}=>\widehat{DCM}=\widehat{LCA}\)
ta có\(\widehat{NCA}=\widehat{LCA}\left(=\widehat{DCM}\right)\)
=> hai tia CN , CL trùng nhau .zậy C,N,L thẳng hàng
Bài 5:Cho tam giác ABC vuông tại A, có AB 8 cm; AC 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.a)Tính độ dài đoạn BC và AMb)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.c) Chứng minh tứ giác OACE nội tiếp Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (MBC, NAC). Hai đường cao AM và BN cắt nhau tại H.a)Chứng minh rằng tứ giác CMHN nội tiếp một đường trònb)Chứng minh rằng AM.CH AC.MN
Đọc tiếp
Bài 5:Cho tam giác ABC vuông tại A, có AB = 8 cm; AC = 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.
a)Tính độ dài đoạn BC và AM
b)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.
c) Chứng minh tứ giác OACE nội tiếp
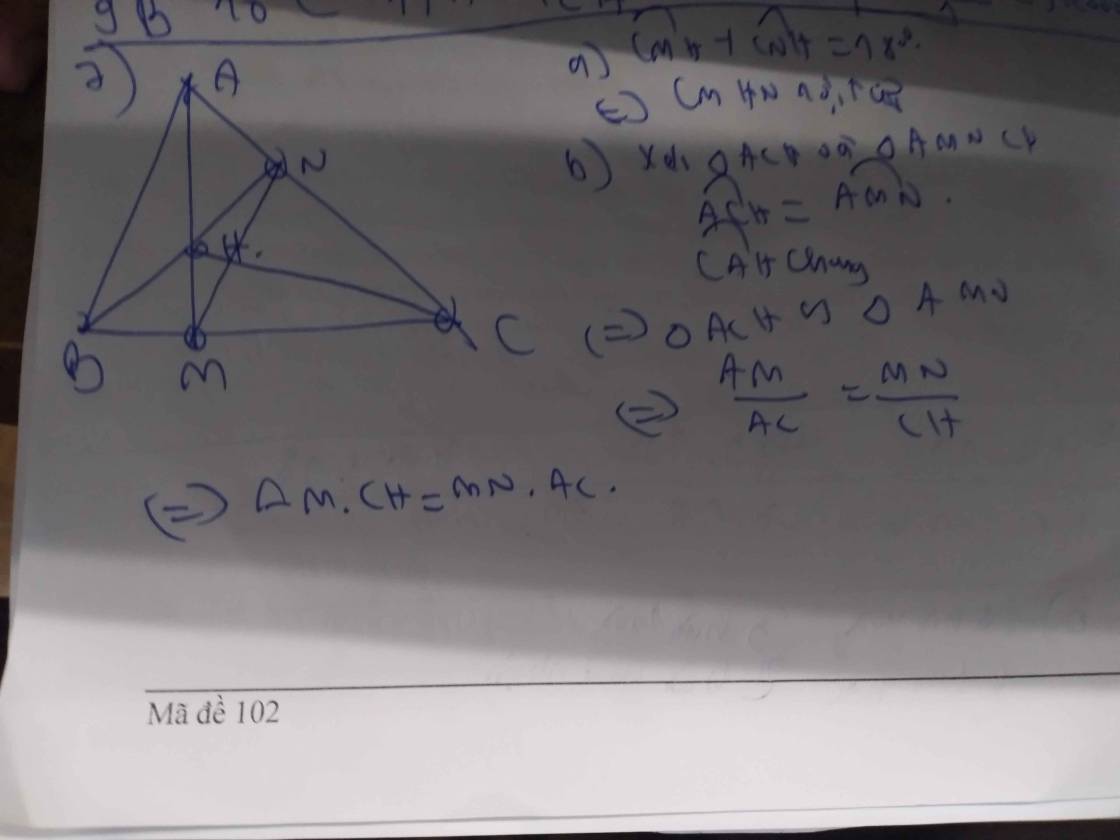
Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (M=BC, N=AC). Hai đường cao AM và BN cắt nhau tại H.
a)Chứng minh rằng tứ giác CMHN nội tiếp một đường tròn
b)Chứng minh rằng AM.CH = AC.MN
tam giác ABC cân tại A vẽ đường tròn (O;R) tiếp xúc AB ,AC tại B , C . Đường thẳng qua điểm M trên BC vuông góc với OM cắt tia AB, AC tại D,E
a, CM 4 điểm O,B,D,M thuộc1 đg tròn
b, CM MD=ME
HELP
Đường thẳng qua M trên cung BC vuông với OM mới đúng chứ bạn
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O bán kính R tiếp xúc với AB,AC tại B,C.Đường thẳng qua điểm m trên BC vuông góc OM cắt tia AB,AC tại D,E
a) CM: 4 điểm O,B,D,M cùng thuộc 1 đường tròn
b) CM: MD=ME
Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O bán kính R tiếp xúc với AB,AC tại B,C.Đường thẳng qua điểm m trên BC vuông góc OM cắt tia AB,AC tại D,E
a) CM: 4 điểm O,B,D,M cùng thuộc 1 đường tròn
b) CM: MD=ME
cho tam giác abc vuông cân tại a có ab=8 cm, ac=6 cm, gọi M là trung điểm của BC. a) cmr: ac và đường tròn ( M;4 cm) tiếp xúc nhau B) cmr: ab và đường tròn tâm (M;4 cm) cắt nhau tại 2 điểm D, E. tính ad và be
Cho tam giác ABC (ABAC) nội tiếp đường tròn đường kính BC , đường cao AH . Gọi I là giao điểm các đường phân giác . Tia phân giác góc AHB cắt tia BI tại J , tia phân giác của góc AHC cắt CI tại K . cm tam giác ABC đồng dạng tam giác HJK Cho (O) đường kính BC , điểm A bất kỳ thuộc (O) : ABAC. Kẻ dây AD vuông góc với BC , các đường thẳng AC và BDF cắt nhau tại E . Từ E kẻ EH vuông góc với BC tại H . cm khi A di chuyển trên (O) : ABAC thì HA luôn tiếp xúc với đường tròn cố địnhAi đúng mình cho 4 ti...
Đọc tiếp
Cho tam giác ABC (AB<AC) nội tiếp đường tròn đường kính BC , đường cao AH . Gọi I là giao điểm các đường phân giác . Tia phân giác góc AHB cắt tia BI tại J , tia phân giác của góc AHC cắt CI tại K . cm tam giác ABC đồng dạng tam giác HJK
Cho (O) đường kính BC , điểm A bất kỳ thuộc (O) : AB<AC. Kẻ dây AD vuông góc với BC , các đường thẳng AC và BDF cắt nhau tại E . Từ E kẻ EH vuông góc với BC tại H . cm khi A di chuyển trên (O) : AB<AC thì HA luôn tiếp xúc với đường tròn cố định
Ai đúng mình cho 4 tick nha
Cho tam giác ABC (ABAC) nội tiếp đường tròn đường kính BC , đường cao AH . Gọi I là giao điểm các đường phân giác . Tia phân giác góc AHB cắt tia BI tại J , tia phân giác của góc AHC cắt CI tại K . cm tam giác ABC đồng dạng tam giác HJK Cho (O) đường kính BC , điểm A bất kỳ thuộc (O) : ABAC. Kẻ dây AD vuông góc với BC , các đường thẳng AC và BDF cắt nhau tại E . Từ E kẻ EH vuông góc với BC tại H . cm khi A di chuyển trên (O) : ABAC thì HA luôn tiếp xúc với đường tròn cố địnhAi đúng mình cho 4 ti...
Đọc tiếp
Cho tam giác ABC (AB<AC) nội tiếp đường tròn đường kính BC , đường cao AH . Gọi I là giao điểm các đường phân giác . Tia phân giác góc AHB cắt tia BI tại J , tia phân giác của góc AHC cắt CI tại K . cm tam giác ABC đồng dạng tam giác HJK
Cho (O) đường kính BC , điểm A bất kỳ thuộc (O) : AB<AC. Kẻ dây AD vuông góc với BC , các đường thẳng AC và BDF cắt nhau tại E . Từ E kẻ EH vuông góc với BC tại H . cm khi A di chuyển trên (O) : AB<AC thì HA luôn tiếp xúc với đường tròn cố định
Ai đúng mình cho 4 tick nha