c. 

Tứ giác IKNC là tứ giác nội tiếp (cmt)=> \(\widehat{IKC}=\widehat{INC}\)(cùng = \(\frac{1}{2}sđ\widebat{IC}\))

Xét đt(O) có: \(\widehat{ABC}=\widehat{ANC=}\widehat{INC}\)(cùng = \(\frac{1}{2}sđ\widebat{NC}\))

=> \(\widehat{ABC}=\widehat{IKC}\)mà 2 góc này ở vị trí đồng vị => IK // HB (dhnb)

Chứng minh tương tự câu a ta có: Tứ giác AMHI là tứ giác nội tiếp => \(\widehat{AHI}=\widehat{AMI}=\widehat{AMC}\)(cùng = \(\frac{1}{2}sđ\widebat{AI}\))

Xét đt(O) có: \(\widehat{ABC}=\widehat{AMC}\left(=\frac{1}{2}sđ\widebat{AC}\right)\)=> \(\widehat{ABC}=\widehat{AHI}\)mà 2 góc này ở vị trí đồng vị => HI // BK

Vì M là điểm chính giữa cung nhỏ \(\widebat{AB}\)(gt) => \(sđ\widebat{AM}=sđ\widebat{BM}\)

Xét đt(O) có: \(\widehat{ACM}=\frac{1}{2}sđ\widebat{AM}\)và \(\widehat{BCM}=\frac{1}{2}sđ\widebat{BM}\)=> \(\widehat{ACM}=\widehat{BCM}\)=> CM là tia phân giác của \(\widehat{ACB}\)

CMTT ta có: AN là tia phân giác của \(\widehat{BAC}\)

Mà 2 dây AN và CM cắt nhau tại I (gt) => BI là tia phân giác của \(\widehat{ABC}\)hay BI là tia phân giác của \(\widehat{HBK}\)

Xét tứ giác BHIK có:

* HI // BK (cmt)

* IK // HB (cmt)

=> tứ giác BHIK là hình bình hành (DHNB)

Mà BI là phân giác của \(\widehat{HBK}\)(cmt) => tứ giác BHIK là hình thoi (dhnb hình thoi)

d. Vì \(\widehat{NBK}=\widehat{BMN}=\widehat{BMK}\left(cmt\right)\)=> BN là tiếp tuyến tại B của đt (P) ngoại tiếp \(\Delta MBK\)=> \(BN\perp BP\)Mà \(BN\perp BD\)do \(\widehat{DBN}=90^o\)(góc nội tiếp chắn nửa đt) => B, P , D thẳng hàng

Tương tự ta có: C, Q, D thẳng hàng

\(\Delta BPK\)và \(\Delta DBC\)là 2 tam giác cân có chung góc ở đáy => góc ở đỉnh của chúng bằng nhau => \(\widehat{BPK}=\widehat{BDC}\)Mà 2 góc này ở vị trí đồng vị => PK // DC (dhnb) => PK // DQ

CMTT ta có: DP // QK => DPKQ  là hình bình hành (dhnb HBH) => DK đi qua trung điểm của PQ => D, E, K thẳng hàng (đpcm)

a. Vì M là điểm chính giữa cung nhỏ \(\widebat{AB}\)(gt) => \(sđ\widebat{AM}=sđ\widebat{MB}\)=> \(\widehat{ACM}=\widehat{BCM}\)(2 góc nội tiếp chắn 2 cung = nhau)

Lại có: \(\widehat{ACM}=\widehat{ANM}\)(CÙNG = \(\frac{1}{2}sđ\widebat{AM}\))  => \(\widehat{MNA}=\widehat{BCM}\)hay \(\widehat{KNI}=\widehat{KCI}\)(Do M,K,N và A,I,N => \(\widehat{MNA}=\widehat{KNI}\); M,I,C và B,K,C => \(\widehat{BCM}=\widehat{KCI}\)) => IKNC là tứ giác nội tiếp (Dấu hiệu nhận biết)

b. Xét đường tròn (O) có: \(\widehat{BMN}=\frac{1}{2}sđ\widebat{BN}\)và \(\widehat{NBC}=\widehat{NBK}=\frac{1}{2}sđ\widebat{NC}\)

mà N là điểm chính giữa cung nhỏ \(\widebat{BC}\)(gt) => sđ \(\widebat{BN}\)= sđ \(\widebat{NC}\)=> \(\widehat{BMN}=\widehat{NBK}\)

Xét \(\Delta BMN\)và \(\Delta KBN\)có:

* \(\widehat{N}\)chung

* \(\widehat{BMN}=\widehat{NBK}\)(cmt)

=> \(\Delta BMN~\Delta KBN\)(g.g) => \(\frac{NB}{NK}=\frac{NM}{NB}\)<=> \(NB^2=NK.NM\)(đpcm)

a: Xét (O) có

ΔAKB nội tiếp

AB là đường kính

Do đó: ΔAKB vuông tại K

Xét tứ giác AECK có \(\widehat{AEC}+\widehat{AKC}=90^0+90^0=180^0\)

nên AECK là tứ giác nội tiếp

b: Xét ΔIAB có

BK,IE là các đường cao

BK cắt IE tại C

Do đó: C là trực tâm của ΔIAB

=>AC\(\perp\)IB tại D

Xét tứ giác CEBD có \(\widehat{CEB}+\widehat{CDB}=90^0+90^0=180^0\)

nên CEBD là tứ giác nội tiếp

Xét tứ giác AKCE có \(\widehat{AKC}+\widehat{AEC}=90^0+90^0=180^0\)

nên AKCE là tứ giác nội tiếp

Xét tứ giác IKCD có \(\widehat{IKC}+\widehat{IDC}=90^0+90^0=180^0\)

nên IKCD là tứ giác nội tiếp

Ta có: \(\widehat{DKC}=\widehat{DIC}\)(DIKC nội tiếp)

\(\widehat{EKC}=\widehat{EAC}\)(KAEC nội tiếp)

mà \(\widehat{DIC}=\widehat{EAC}\left(=90^0-\widehat{DBA}\right)\)

nên \(\widehat{DKC}=\widehat{EKC}\)

=>KC là phân giác của góc DKE

Ta có: \(\widehat{KDC}=\widehat{KIC}\)(DIKC là tứ giác nội tiếp)

\(\widehat{EDC}=\widehat{EBC}\)(EBDC nội tiếp)

mà \(\widehat{KIC}=\widehat{EBC}\left(=90^0-\widehat{KAB}\right)\)

nên \(\widehat{KDC}=\widehat{EDC}\)

=>DC là phân giác của góc KDE

Xét ΔKED có

DC,KC là các đường phân giác

Do đó: C là tâm đường tròn nội tiếp ΔKED

=>C cách đều ba cạnh của ΔKED

4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác  B D C ^

Ta có  K Q C ^ = 2 K M C ^  (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))

N D C ^ = K M C ^  (góc nội tiếp cùng chắn cung  N C ⏜ )

Mà  B D C ^ = 2 N D C   ^ ⇒ K Q C ^ = B D C ^

Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở  ⇒ B C D ^ = B C Q ^  do vậy D, Q, C thẳng hàng nên KQ//PK

Chứng minh tương tự ta có  ta có D, P, B thẳng hàng và DQ//PK

Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).

 gọi O là tâm đường tròn đường kính AB 

Kẻ OE vuông góc vs CD (E thuộc CD)

 suy ra E là trung điểm của CD 

Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song vs cạnh đáy)

suy ra EH=EK mà EC=ED Suy ra đpcm

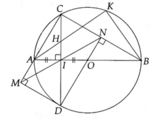
a,  H I B ^ = H K B ^ = 180 0

=> Tứ giác BIHK nội tiếp

b, Chứng minh được: DAHI ~ DABK (g.g)

=> AH.AK = AI.AB = R 2 (không đổi)

c, Chứng minh được MCND là hình chữ nhật từ đó => Đpcm