Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
![]()
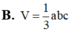
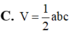
![]()
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
![]()
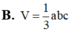
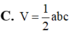
![]()
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
A. V = a b c
B. V = 1 3 a b c
C. V = 1 2 a b c
D. V = 3 a b c
Một hình hộp chữ nhật có ba kích thước là a, b, c. Thể tích V của khối hộp chữ nhật đó bằng
A.(a+b)c
B. 1 3 a b c
C. abc
D.(a+c)b
Một hình hộp chữ nhật có ba kích thước là a , b , c . Thể tích V của khối hộp chữ nhật đó bằng
A. a + c b
B. a b c
C. a + b c
D. 1 3 a b c
Một hình hộp chữ nhật có ba kích thước a , b , c . là V Thể tích của khối hộp chữ nhật đó bằng
A. a + c b .
B. a b c .
C. a + b c .
D. 1 3 a b c .
Một hình hộp chữ nhật có kích thước a ( c m ) x b ( c m ) x c ( c m ) trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi v ( c m 3 ) và s ( c m 2 ) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = s tìm số các bộ ba số ( a , b , c ) .
A. 4
B. 10
C. 12
D. 21
Một hình hộp chữ nhật có kích thước a (cm) × b (cm) × c (cm), trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi S (cm3) và S (cm2) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = S , tìm số các bộ ba số a , b , c ?
A. 4
B. 10
C. 12
D. 21
Đáp án B.
Ta có V = a b c S = 2 a b + b c + c a . Theo đề ta có:
a b c = 2 a b + b c + c a ; 1 ≤ a ≤ b ≤ c ⇔ 1 = 2. a b + b c + c a a b c ⇔ 2 a + 2 b + 2 c = 1
Ta có 1 = 2 a + 2 b + 2 c ≤ 2 a + 2 a + 2 a = 6 a ⇒ a ≤ 6 . Kết hợp với 2 a + 2 b + 2 c = 1 ta có:
a = 3 ⇒ 1 b + 1 c = 1 6 ⇒ 6 < b ≤ 12
⇒ a ; b ; c e { 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 }
Với a = 4 ⇒ 1 b + 1 c = 1 4 ⇒ 4 < b ≤ 8 ⇒ a ; b ; c ∈ 4 ; 5 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8
với a = 5 ⇒ 1 b + 1 c = 3 10 < 1 3 ⇒ b < 6 ⇒ a ; b ; c ∈ 5 ; 5 ; 10
với a = 6 ⇒ 1 b + 1 c = 1 3 ⇒ b ≤ 6 ⇒ a ; b ; c ∈ 6 ; 6 ; 6
⇒ a ; b ; c ∈ 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 4 ; 6 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8 , 5 ; 5 ; 10 , 6 ; 6 ; 6
Vậy ta chọn B.
Một hình hộp chữ nhật có kích thước a c m × b c m × c c m , trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi V c m 3 và S c m 2 lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = S tìm số các bộ ba số (a,b,c)
A. 4
B. 10
C. 12
D. 21
I. Trắc nghiệm ( 6 điểm)
Một hình hộp chữ nhật có ba kích thước là a, b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, b, c.
A. π a 2 + b 2 + c 2
B. 2 π a 2 + b 2 + c 2
C. 4 π a 2 + b 2 + c 2
D. π 2 a 2 + b 2 + c 2
Chọn A.
Tâm của mặt cầu chính là tâm của của hình hộp chữ nhật.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật.
Mà độ dài đường chéo của hình chữ nhật là ![]() nên mặt cầu (S) có bán kính
nên mặt cầu (S) có bán kính
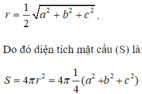
![]()
Một hình hộp chữ nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của hình cầu (S) theo a, b, c bằng
A. π 2 a 2 + b 2 + c 2
B. 4 π a 2 + b 2 + c 2
C. π a 2 + b 2 + c 2
D. 2 π a 2 + b 2 + c 2
Mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật có tâm là tâm của hình hộp chữ nhật đó và có bán kính bằng nửa độ dài đường chéo của hình hộp
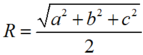
Diện tích của hình cầu đó là:
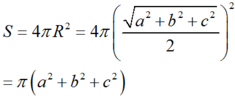
Chọn: C