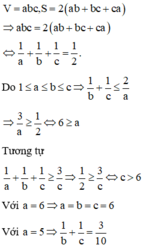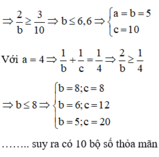Các câu hỏi tương tự
Một hình hộp chữ nhật có kích thước a (cm) × b (cm) × c (cm), trong đó a, b, c là các số nguyên và
1
≤
a
≤
b
≤
c
. Gọi S (cm3) và S (cm2) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết
V
S
, tìm số các bộ ba số
a
,
b
,
c
? A. 4 B. 10 C. 12 D. 21
Đọc tiếp
Một hình hộp chữ nhật có kích thước a (cm) × b (cm) × c (cm), trong đó a, b, c là các số nguyên và 1 ≤ a ≤ b ≤ c . Gọi S (cm3) và S (cm2) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết V = S , tìm số các bộ ba số a , b , c ?
A. 4
B. 10
C. 12
D. 21
Một hình hộp chữ nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của hình cầu (S) theo a, b, c bằng A.
π
2
a
2
+
b
2
+
c
2
B.
4
π
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của hình cầu (S) theo a, b, c bằng
A. π 2 a 2 + b 2 + c 2
B. 4 π a 2 + b 2 + c 2
C. π a 2 + b 2 + c 2
D. 2 π a 2 + b 2 + c 2
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức: A.
V
a
b
c
B.
V
1
3
a
b
c
C.
V
1
2
a
b
c
D.
V
3
a
b
c
Đọc tiếp
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
A. V = a b c
B. V = 1 3 a b c
C. V = 1 2 a b c
D. V = 3 a b c
Một hình hộp chữ nhật có ba kích thước là a, b, c. Thể tích V của khối hộp chữ nhật đó bằng
A.(a+b)c
B. 1 3 a b c
C. abc
D.(a+c)b
Một hình hộp chữ nhật có ba kích thước
a
,
b
,
c
.
là V Thể tích của khối hộp chữ nhật đó bằng A.
a
+
c
b
.
B.
a
b
c
.
C.
a
+
b
c
.
D. ...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước a , b , c . là V Thể tích của khối hộp chữ nhật đó bằng
A. a + c b .
B. a b c .
C. a + b c .
D. 1 3 a b c .
Cho hình hộp chữ nhật ABCD.A B C D có các kích thước là AB2, AD3, AA4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB A và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là A.
5
π
B.
13
π
3
C.
8
π
D.
25
π
6
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A' B' C' D' có các kích thước là AB=2, AD=3, AA'=4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB' A' và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
A. 5 π
B. 13 π 3
C. 8 π
D. 25 π 6
Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị
C
:
y
−
x
3
+
6
x
2
−
9
x
+
2
tại ba điểm phân biệt A,B,C Gọi B,C lần lượt là hình chiếu vuông góc của B,C lên trục tung. Tìm giá trị dương của m để hình thang BBCC có diện tích A. m1 B.
m
1
2...
Đọc tiếp
Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị C : y = − x 3 + 6 x 2 − 9 x + 2 tại ba điểm phân biệt A,B,C Gọi B',C' lần lượt là hình chiếu vuông góc của B,C lên trục tung. Tìm giá trị dương của m để hình thang BB'C'C có diện tích
A. m=1
B. m = 1 2
C.m=2
D. m = 3 2
Một hình hộp chữ nhật có ba kích thước là a, b, c nội tiếp một mặt cầu. Khi đó diện tích
S
m
c
của mặt cầu đó là A.
S
m
c
16
a
2
+
b
2
+
c
2...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước là a, b, c nội tiếp một mặt cầu. Khi đó diện tích S m c của mặt cầu đó là
A. S m c = 16 a 2 + b 2 + c 2 π
B. S m c = 8 a 2 + b 2 + c 2 π
C. S m c = 4 a 2 + b 2 + c 2 π
D. S m c = a 2 + b 2 + c 2 π
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD8,CD6,AC12. Tính diện tích toàn phần
S
t
p
của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′. A.
S
t
p
576
π
B.
S
t
p
10
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD=8,CD=6,AC'=12. Tính diện tích toàn phần S t p của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′.
A. S t p = 576 π
B. S t p = 10 2 11 + 5 π
C. S t p = 26 π
D. S t p = 5 4 11 + 5 π