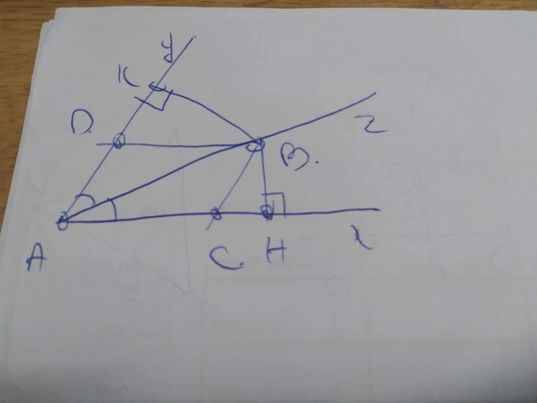
Cho tam giác ABC có góc B=C=40 độ. Vẽ Ax là tia phân giác ngoài tại đỉnh A. Ay là tia phân giác trong tại đỉnh A. Đg thẳng bất kì đi qua C cắt Ax tại M . Cắt Ay tại N . Vẽ Ak vông với MN
a, Chứng minh rằng Ax // BC và AM vuông với AN
b, CMR góc MAK = MNA
c, CMR góc NAK = AMK
Giúp mk với