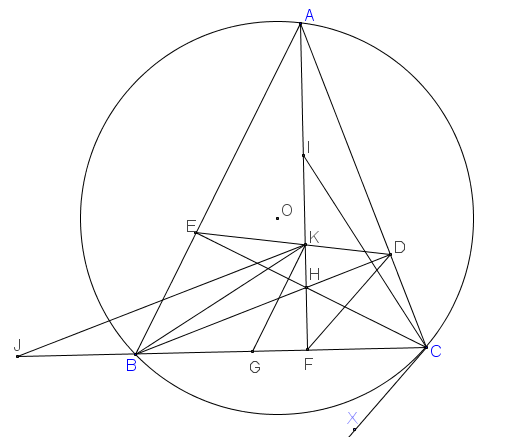
Cho tam giác nhọn ABC. VẼ đường tròn (O) đường kính BC, H là trực tâm tam giác ABC. Vẽ các tiếp tuyến AD, AE của đường tròn (O) (D và E thuộc cùng một nửa mặt phẳng bờ AH). CMR: AH, BD, CE đồng quy

Những câu hỏi liên quan
Cho tam giác ABC nhọn có AB < AC, đường cao AD. Đường tròn tâm ),đường kính BC. Vẽ AM và AN là hai tiếp tuyến của đường tròn.
a. Chứng minh 5 điểm M, N, O, D. A cùng thuộc một đường tròn
b. Gọi MN cắt AD tại H. Chứng minh H là trực tâm tam giác ABC
a) Ta có: \(\widehat{AMO}=\widehat{ADO}=\widehat{ANO}=90^o\) nên \(M,N,D\) cùng nhìn \(AO\) dưới một góc vuông suy ra \(M,D,O,N,A\) cùng thuộc một đường tròn.
b) Gọi \(F\) là giao điểm của \(AC\) và đường tròn \(\left(O\right)\).
\(\Delta ANF\sim\Delta ACN\left(g.g\right)\) suy ra \(AN^2=AC.AF\).
Xét tam giác \(AHN\) và tam giác \(AND\):
\(\widehat{HAN}=\widehat{NAD}\) (góc chung)
\(\widehat{ANH}=\widehat{ADN}\) (vì \(AMDON\) nội tiếp, \(\widehat{ANH},\widehat{ADN}\) chắn hai cung \(\stackrel\frown{AM},\stackrel\frown{AN}\) mà \(AM=AN\))
\(\Rightarrow\Delta AHN\sim\Delta AND\left(g.g\right)\)
suy ra \(AN^2=AH.AD\)
suy ra \(AC.AF=AH.AD\)
\(\Rightarrow\Delta AFH\sim\Delta ADC\left(c.g.c\right)\Rightarrow\widehat{AFH}=\widehat{ADC}=90^o\)
suy ra \(\widehat{HFC}=90^o\) mà \(\widehat{BFC}=90^o\) (do \(F\) thuộc đường tròn \(\left(O\right)\))
suy ra \(B,H,F\) thẳng hàng do đó \(BH\) vuông góc với \(AC\).
Tam giác \(ABC\) có hai đường cao \(AD,BF\) cắt nhau tại \(H\) suy ra \(H\) là trực tâm tam giác \(ABC\).
Đúng 1
Bình luận (0)
Bạn check lại và đánh lại đề để mình có thể giúp đỡ nha.
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm (O) đường kính BC ,vẽ tam giác ABC nhọn(điểm A nằm ngoài nửa đường tròn ,A thuộc cùng nửa mặt phẳng với nửa đường tròn có bờ BC) ,AB và AC cắt nửa đường tròn tại D và E ,H là giao điểm của BE và CD ,F là giao điểm của BH và CDCm:a)tứ giác ADHE là tứ giác nội tiếp b) cm AE.AC=AB.AD
AI GIÚP MK VS :((
a) Xét (O) có
ΔBDC nội tiếp đường tròn(B,D,C∈(O))
BC là đường kính(gt)
Do đó: ΔBDC vuông tại D(Định lí)
⇔CD⊥BD tại D
⇔CD⊥AB tại D
⇔\(\widehat{ADC}=90^0\)
hay \(\widehat{ADH}=90^0\)
Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C∈(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
⇔BE⊥CE tại E
⇔BE⊥AC tại E
⇔\(\widehat{AEB}=90^0\)
hay \(\widehat{AEH}=90^0\)
Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔABE vuông tại E và ΔACD vuông tại D có
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACD(g-g)
⇔\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB\cdot AD=AC\cdot AE\)(đpcm)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC nội tiếp đường tròn (O) (AB AC). hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AE của đường tròn (O) . Gọi I là trung điểm BC. Chứng minh rằng:a, B, E, D, C cùng thuộc đường tròn (I) và AE. AB AD. ACb, tứ giác BHCF là hình gì? CMR: OH 2OIc, CÁc tiếp tuyến tại D, E của đường tròn (i) đường kính BC và AH đồng quyd, Cho biết widehat{ABC}60
, widehat{ACH}45 Tính diện tích tam giác ABC theo a Giúp mk vs nà m.n ơi!!! cảm ơn m.n nhìu ạ
Đọc tiếp
Bài 1: Cho tam giác ABC nội tiếp đường tròn (O) (AB< AC). hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AE của đường tròn (O) . Gọi I là trung điểm BC. Chứng minh rằng:
a, B, E, D, C cùng thuộc đường tròn (I) và AE. AB= AD. AC
b, tứ giác BHCF là hình gì? CMR: OH= 2OI
c, CÁc tiếp tuyến tại D, E của đường tròn (i) đường kính BC và AH đồng quy
d, Cho biết \(\widehat{ABC}=60
\), \(\widehat{ACH}=45\)
Tính diện tích tam giác ABC theo a
Giúp mk vs nà m.n ơi!!! cảm ơn m.n nhìu ạ
Cho tam giác ABC có 3 góc nhọn, nội tiếp đường tròn tâm O và AB<AC. Vẽ đường kính AD của đường tròn (O). Kẻ BE và CF vuông góc với AD( E,F thuộc AD). Kẻ AH vuông góc với AC(H thuộc BC).
a) Chứng minh 4 điểm A,B,H,E cùng nằm trên một đường tròn và tam giác ABH đồng dạng với tam giác ADC.
b) Chứng minh HE // CD
c) Gọi M là trung điểm của BC. Chuwngd minh ME=MF.
a: góc AEB=góc AHB=90 độ
=>AEHB nội tiếp
Xét ΔAHB vuông tại H và ΔACD vuông tại C có
góc ABH=góc ADC
=>ΔAHB đồng dạng với ΔACD
b: góc HAC+góc AHE
=góc ABE+90 độ-góc HAB
=90 độ
=>HE vuông góc AC
=>HE//CD
Đúng 1
Bình luận (0)
cho tam giác nhọn ABC( AB<AC) đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và D . CE cắt BD ở H và AH cắt BC ở K.
a) BEHK nội tiếp và KA là tia phân giác của góc EKD
b) gọi AI , AJ là tiếp tuyến của đường tròn (O) ; (I,J là các tiếp điểm và hai điểm D J nằm cùng một nửa mặt phẳng bờ là AK ) chứng minh rằng góc IKE= góc DKJ
c) ba điểm I ; H ; J thẳng hàng .
a) Tứ giác BEHK có hai góc đỉnh E, K là vuông nên bốn đỉnh của tứ giác thuộc đường tròn đường kính EK.
Mặt khác, tứ giác ABKD có bốn đỉnh nằm trên đường tròn đường kính AB. Theo tính chất về các góc nội tiếp cùng chắn một cung thì bằng nhau, ta suy ra \(\angle EKA=\angle EBD=\angle AKD\to AK\) là phân giác của góc EKD.
b) Tứ giác AIKJ có hai góc đỉnh I, J vuông nên các đỉnh của tứ giác nằm trên đường tròn đường kính AK. Do vậy \(\angle IKA=\angle AJI,\angle JKA=\angle AIJ\to\angle IKA=\angle JKA\) (do tính chất tiếp tuyến). Mà AK là phân giác của góc EKD. Suy ra \(\angle IKE=\angle JDA.\)
c) Gọi T là giao điểm AO với IJ. Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu trong tam giác vuông, ta có
\(AI^2=AT\cdot AO.\) Do chứng minh trên
\(\angle IKA=\angle AJI=\angle AIJ\to\Delta AIH\sim\Delta AKI\left(g.g\right)\to\frac{AI}{AK}=\frac{AH}{AI}\to AI^2=AH\cdot AK.\)
Vậy ta có \(AT\cdot AO=AH\cdot AK\to\frac{AT}{AH}=\frac{AK}{AO}\to\Delta ATK\sim\Delta AKO\to\angle ATH=\angle AKO=90^{\circ}.\) Do đó ta có \(HT\perp AO\), mà \(IJ\perp AO\) do tính chất tiếp tuyến. Suy ra \(TH\equiv IJ\to I,H,J\) thẳng hàng.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AHh. Vẽ đường tròn tâm A bán kính AH. Kẻ các tiếp tuyến BD, CE với đường tròn O(D và E khác H)
a) Chứng minh O,A,E thẳng hàng
b) DE tiếp xúc với đường tròn đường kính BC
Cho tam giác ABC nhọn nội tiếp đường tròn (O) (AB<AC). Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn, AD cắt BC tại E. Gọi K là chân đường vuông góc kẻ từ C đến ADa) C/m 4 điểm A, H, K, C cùng thuộc một đường tròn
Xem chi tiết
a: Xét tứ giác AHKC có \(\widehat{AHC}=\widehat{AKC}=90^0\)
nên AHKC là tứ giác nội tiếp
=>A,H,K,C cùng thuộc một đường tròn
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn (AB AC) nội tiếp (O; R), các đường cao BD, CE cắt nhau tạiH. AH cắt BC, DE lần lượt tại F và K.a) Chứng minh rằng tứ giác ADHE nội tiếp đường tròn, xác định tâm I của đường tròn này.b) Vẽ tia Cx là tiếp tuyến của (O) (tia Cx nằm trên nửa mặt phẳng bờ BC không chứa điểmA). Chứng minh rằng tứ giác ADFB nội tiếp đường tròn và Cx // DF.c) Chứng minh rằng DH là tia phân giác của góc EDF và AF.HK AK.HF.d) Chứng minh tam giác FBK đồng dạng tam giác FIC rồi suy ra K là trực tâm...
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) nội tiếp (O; R), các đường cao BD, CE cắt nhau tạiH. AH cắt BC, DE lần lượt tại F và K.
a) Chứng minh rằng tứ giác ADHE nội tiếp đường tròn, xác định tâm I của đường tròn này.
b) Vẽ tia Cx là tiếp tuyến của (O) (tia Cx nằm trên nửa mặt phẳng bờ BC không chứa điểmA). Chứng minh rằng tứ giác ADFB nội tiếp đường tròn và Cx // DF.
c) Chứng minh rằng DH là tia phân giác của góc EDF và AF.HK = AK.HF.
d) Chứng minh tam giác FBK đồng dạng tam giác FIC rồi suy ra K là trực tâm tam giác BIC
*Sửa giúp em câu c & d ạ
d)
Trên BF lấy điểm G sao cho GK //AB
=>KG⊥⊥CE (1) và BGBF=AKAFBGBF=AKAF (2)
theo câu c), DH là phân giác trong ˆKDFKDF^ (3)
=>HKHF=DKDFHKHF=DKDF (4)
có DA⊥⊥DH (5)
từ (3, 5) =>DA là phân giác ngoài ˆKDFKDF^
=>AKAF=DKDFAKAF=DKDF (6)
từ (2, 4, 6) =>BGBF=HKHFBGBF=HKHF (7)
trên tia đối tia BC lấy điểm J sao cho BJ =BG
=>BJBF=BGBFBJBF=BGBF (8)
từ (7, 8) =>BJBF=HKHFBJBF=HKHF
=>JK // BH
=>JK⊥⊥AC (8)
từ (1, 8) =>ˆJKG=ˆACHJKG^=ACH^ (9)
và có JF⊥⊥AH và (1)=>ˆKGJ=ˆCHAKGJ^=CHA^ (10)
từ (9, 10) =>△KGJ∼△CHA△KGJ∼△CHA (g, g)
=>KGCH=GJHA=2.GB2.HI=GBHIKGCH=GJHA=2.GB2.HI=GBHI (11)
từ (10, 11) =>△KGB∼△CHI△KGB∼△CHI (c, g, c)
=>ˆKBF=ˆCIFKBF^=CIF^
=>△FBK∼△FIC△FBK∼△FIC (đpcm)
và ˆICB+ˆFBKICB^+FBK^
=ˆBKF+ˆFBK=90∘=BKF^+FBK^=90∘
=>BK⊥CIBK⊥CI =>K là trực tâm của tam giác IBC (đpcm)
Hình gửi kèm
Cho tam giác ABC nhọn nội tiếp trong đường tròn (O;R) . Vẽ đường kính AD và đường cao AH của tam giác ABC .1/ CMR : AB.ACAH.AD2/đường thẳng AH cắt đường tròn (O) tại E . Gọi K là điểm đối xứng của E qua BC . CMR K là trực tâm của tam giác ABC .3/ hai đường thẳng CK và AB cắt nhau tại M . Hai đường thẳng BK và AC cắt nhau tại N . CMR : AD vuông góc với MN . 4/ cho góc BAC 45 độ CMR : 5 điểm B,M ,N O,C cùng thuộc một đường tròn tâm I . Tính diện tích hình phẳng giới hạn bởi dây MN và cung MN của...
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp trong đường tròn (O;R) . Vẽ đường kính AD và đường cao AH của tam giác ABC .
1/ CMR : AB.AC=AH.AD
2/đường thẳng AH cắt đường tròn (O) tại E . Gọi K là điểm đối xứng của E qua BC . CMR K là trực tâm của tam giác ABC .
3/ hai đường thẳng CK và AB cắt nhau tại M . Hai đường thẳng BK và AC cắt nhau tại N . CMR : AD vuông góc với MN .
4/ cho góc BAC = 45 độ CMR : 5 điểm B,M ,N O,C cùng thuộc một đường tròn tâm I . Tính diện tích hình phẳng giới hạn bởi dây MN và cung MN của đường tròn (I) theo R .
Chỉ giúp mình câu 4/ nha !
cho mình biết hình phẳng giới hạn là cái hell gì có được không
Đúng 0
Bình luận (0)
câu 4 mình k biết lạm bạn ới chả biết hình j
Đúng 0
Bình luận (0)
Cho mình nói ngoài lề đi,bạn cung giỏi toán đúng k,bạn ở tỉnh nào,cũng đang trong giai đoạn ôn thi thì tụi ình kết bạn facebook đi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
















