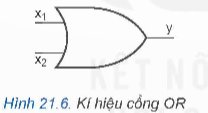
Vẽ sơ đồ logic của hàm y = (x1 + x2) + x3 sử dụng kí hiệu logic trong Hình 21.6.
Sử dụng tư duy logic của mình để tìm số còn thiếu trong sơ đồ dưới đây.

TL:
Vì 7 + 3 = 10 : 2 = 5 nên ta có thể suy luận ra:
Lấy 4 + 2 = 6 : 2 = 3
Đáp án: 3
HT
Biết rằng đồ thị hàm số y = 2 x + 1 x và đồ thị hàm số y = x 3 + x + 1 có hai điểm chung, kí hiệu x 1 , y 1 , x 2 , y 2 là tọa độ hai điểm đó. Tìm y 1 + y 2
A. y 1 + y 2 = 0
B. y 1 + y 2 = 4
C. y 1 + y 2 = 6
D. y 1 + y 2 = 2
Biết rằng đường thẳng y = x - 1 cắt đồ thị hàm số y = x 3 - 3 x 2 + x + 3 tại hai điểm phân biệt; kí hiệu ( x 1 ; y 1 ) , x 2 ; y 2 là tọa độ của hai điểm đó. Tính y 1 + y 2
A. y 1 + y 2 = - 1
B. y 1 + y 2 = 1
C. y 1 + y 2 = - 3
D. y 1 + y 2 = 2
Đáp án A
Hoành độ giao điểm của đt y = x - 1 và đồ thị y = x 3 - 3 x 2 + 4 = 0 là nghiệm của PT
x 3 - 3 x 2 + x + 3 = x - 1 ⇔ ( x + 1 ) ( x - 2 ) 2 = 0 ⇔ x 1 = - 1 x 2 = 2 ⇒ y 1 = - 2 y 2 = 1 ⇒ y 1 + y 2 = - 1
Cho hàm số y=f(x) có đồ thị như hình vẽ bên:
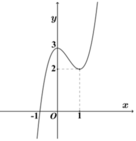
Điều kiện của m để phương trình f x = m có 4 nghiệm phân biệt x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 ≤ - 1 2 x 2 < x 3 ≤ 1 2 x 4 là:
A. m ∈ 2 ; 3
B. m ∈ 2 ; 3
C. m ∈ [ 5 2 ; 3 )
D. m ∈ [ 2 ; 5 2 )
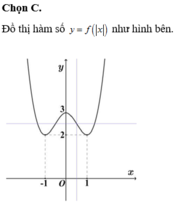
Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị I 1 2 ; 5 2
Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì 5 2 ≤ m < 3
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
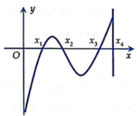
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y = f x . Biết hàm số y = f ' x có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
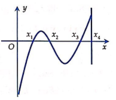
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Đáp án A
Dựa vào đồ thị hàm số y = f ' x , ta có nhận xét:
Hàm số y = f ' x đổi dấu từ – sang + khi qua x = x 1 .
Hàm số y = f ' x đổi dấu từ + sang – khi qua x = x 2 .
Hàm số y = f ' x đổi dấu từ – sang + khi qua x = x 3 .
Từ đó ta có bảng biến thiên của hàm số y = f x trên đoạn 0 ; x 4 như sau:
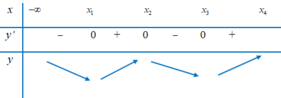
Sử dụng bảng biến thiên ta tìm được max 0 ; x 4 [ f x = max f 0 , f x 2 , f x 4 min 0 ; x 4 f x = min f x 1 , f x 3 .
Quan sát đồ thị, dùng phương pháp tích phân để tính diện tích, ta có:
∫ x 1 x 2 f ' x d x < ∫ x 2 x 3 0 − f ' x d x ⇒ f x 3 < f x 1 ⇒ min 0 ; x 4 f x = f x 3
Tương tự, ta có
∫ 0 x 1 0 − f ' x d x > ∫ x 1 x 2 f ' x d x ⇒ f 0 > f x 2 ∫ x 2 x 3 0 − f ' x d x > ∫ x 3 x 4 f ' x d x ⇒ f x 2 > f x 4
⇒ f 0 > f x 2 > f x 4 ⇒ max 0 ; x 4 f x = f x 3
Vậy max 0 ; x 4 f x = f 0 ; min 0 ; x 4 f x = f x 3
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng![]()
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
C1. Sử dụng các kí hiệu dưới đây, hãy vẽ sơ đồ mạch điện hình 19.3 theo đúng vị trí các bộ phận mạch điện như trên hình này.
C2. Hãy vẽ một sơ đồ khác đã so với sơ đồ đã vẽ ở câu C1 bằng cách thay đổi vị trí các kí hiệu trong sơ đồ này.
C3. Mắc mạch điện như đúng sơ đồ đã vẽ ở cầu C2, tiến hành kiểm tra và đóng công tắc để đảm bảo mạch điện kín và đèn sáng.
C1;
Sơ đồ mạch điện hình 19.3:
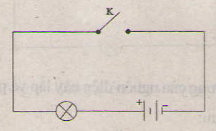
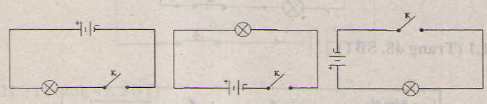
C2:
Các bn mắc mạch điện theo một trong các sơ đồ của câu C2 để kiểm tra
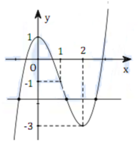
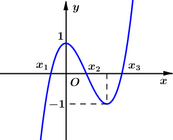
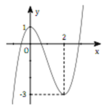
Cho hàm số y = f x = x 3 − 3 x 2 + 1 (C) đồ thị như hình vẽ bên. Với giá trị nào của m thì đường thẳng y = m + 1 cắt (C) tại ba điểm phân biệt có hoành độ x 1 < 1 < x 2 < x 3 ?
A. − 4 < m < 0.
B. − 2 < m < 0.
C. − 4 < m < − 2.
D. m = − 2.
Đáp án C
Em có f(1) = -1. Do đường thẳng y = m +1 có đồ thị là một đường thẳng song song hoặc trùng với trục hoành. Vậy để đường thẳng y = m +1 cắt (C) tại ba điểm phân biệt có hoành độ x 1 < 1 < x 2 < x 3 thì đường thẳng y = m +1 phải cắt đồ thị như hình vẽ
⇔ − 3 < m + 1 < − 1 ⇔ − 4 < m < − 2