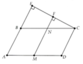
cho tam giác ABC , trục tâm là H , các đường thẳng vuông góc với AB tại B và vuông góc với AC tại C và cắt nhau ở D . chứng minh rằng :
a, tứ giác BDCH là hình bình hành
b, \(\widehat{BAC}\)+ \(\widehat{BDC}\)=180O
c, H, M, D thẳng hàng với M là trung điểm của BC
d, OM = \(\frac{1}{2}\)AH với O là trung điểm của AD