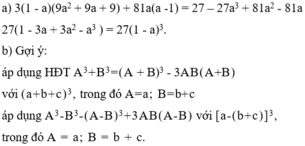√81a với a<0 là bao nhiêu vậy mọi người

Những câu hỏi liên quan
\(\sqrt{9a}+\sqrt{81a}+3\sqrt{25a}-16\sqrt{49a}\) (với a≥0)
\(\sqrt{9a}+\sqrt{81a}+3\sqrt{25a}-16\sqrt{49a}\)
\(=3\sqrt{a}+9\sqrt{a}+15\sqrt{a}+112\sqrt{a}\)
\(=139\sqrt{a}\)
Đúng 1
Bình luận (0)
* Rút gọn:
a.\(\sqrt{\left(\sqrt{7}-4\right)^2+\sqrt{7}}\)
b.\(\sqrt{81a}-\sqrt{144a}+\sqrt{36a}\) với a≥0
`a)sqrt{(sqrt7-4)^2}+sqrt7`
`=|sqrt7-4|+sqrt7`
`=4-sqrt7+sqrt7=4`
`b)\sqrt{81a}-sqrt{144a}+sqrt{36a}(a>=0)`
`=9sqrta-12sqrta+6sqrta=3sqrta`
Đúng 0
Bình luận (0)
a) Ta có: \(\sqrt{\left(\sqrt{7}-4\right)^2}+\sqrt{7}\)
\(=4-\sqrt{7}+\sqrt{7}\)
=4
b) Ta có: \(\sqrt{81a}-\sqrt{144a}+\sqrt{36a}\)
\(=9\sqrt{a}-12\sqrt{a}+6\sqrt{a}\)
\(=3\sqrt{a}\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử: a2-9a3+81a-81
giúp mình với mọi người ơi!!!
\(a^2-9a^3+81a-81\)
Phân tích đa thức thành nhân tử:
\(-\left(9a^3-a^2-81a+81\right)\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức:
a, √45 - √20 - 1/4√80 + √125
b, √81a - √36a - 1/5√25a với a > 0
c, 3√27 - 3√- 8 - 3√-125 -> câu này là căn bậc 3 nhé
\(a,=3\sqrt{5}-2\sqrt{5}-\sqrt{5}+5\sqrt{5}=5\sqrt{5}\\ b,=9\sqrt{a}-6\sqrt{a}-\sqrt{a}=2\sqrt{a}\\ c,Sửa:3\sqrt[3]{27}-3\sqrt[3]{-8}-3\sqrt[3]{-125}\\ =3\cdot3-3\left(-2\right)-3\left(-5\right)\\ =9+6+15=30\)
Đúng 3
Bình luận (0)
Rút gọn biểu thức:a) 3(1 – a)(9
a
2
+ 9a + 9) + 81a(a – 1);b*)
(
a
+
b
+
c
)
3
+
(
a
–
...
Đọc tiếp
Rút gọn biểu thức:
a) 3(1 – a)(9 a 2 + 9a + 9) + 81a(a – 1);
b*) ( a + b + c ) 3 + ( a – b – c ) 3 .
PhÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ:
\(a^4-9a^3+81a-81\)
=a4-81-(9a3-81a)
=(a2-9)(a2+9) -9a(a2-9)
=(a2-9)(a2-9a+9)
ĐẾN ĐÂY MÌNH CHỊU ,BẠN GIẢI TIẾP NHA
Đúng 0
Bình luận (0)
(3a+2b)^2-18a(3a+2b)+81a^2
\(=\left(3a+2b-9a\right)^2=\left(2b-6a\right)^2\)
Đúng 0
Bình luận (0)
phân tích thành nhân tử
`25a^2 -(a-b)^2`
`4a^2 -(a+b)^2`
`49a^2 -(2a-b)^2`
`36a^2-(3a-2b)^2`
`81a^2 -(5a-3b)^2`
a: =(5a-a+b)(5a+a-b)
=(4a+b)(5a-b)
b: =(2a-a-b)(2a+a+b)
=(a-b)(3a+b)
c: =(7a-2a+b)(7a+2a-b)
=(5a+b)(9a-b)
d: =(6a-3a+2b)(6a+3a-2b)
=(3a+2b)(9a-2b)
e: =(9a-5a+3b)(9a+5a-3b)
=(4a+3b)(14a-3b)
Đúng 1
Bình luận (0)
Lời giải:
$25a^2-(a-b)^2=(5a)^2-(a-b)^2=[5a-(a-b)][5a+(a-b)]=(4a+b)(6a-b)$
$4a^2-(a+b)^2=(2a)^2-(a+b)^2=[2a-(a+b)][2a+(a+b)]=(a-b)(3a+b)$
$49a^2-(2a-b)^2=(7a)^2-(2a-b)^2=[7a-(2a-b)][7a+(2a-b)]=(5a+b)(9a-b)$
$36a^2-(3a-2b)^2=(6a)^2-(3a-2b)^2=[6a-(3a-2b)][6a+(3a-2b)]$
$=(3a+2b)(9a-2b)$
$81a^2-(5a-3b)^2=(9a)^2-(5a-3b)^2=[9a-(5a-3b)][9a+(5a-3b)]$
$=(4a+3b)(14a-3b)$
Đúng 1
Bình luận (0)
Viết các số hoặc biểu thức dưới dấu căn thành dạng tích rồi đưa 1 thừa số ra ngoài dấu căn.
√108(a + 7)^2
√81a^4b^7
√16a^5b^3 (a ≥ 0, b ≤ 0)
a: \(\sqrt{36\cdot3\cdot\left(a+7\right)^2}=6\sqrt{3}\left|a+7\right|\)
b: \(\sqrt{9^2\cdot a^4\cdot b^3\cdot b^3\cdot b}=9a^2b^3\sqrt{b}\)
c: Nếu đk xác định như này thì \(C=\sqrt{16a^5b^3}\) chỉ xác định với a=b=0 thôi nha bạn
=>C=0
Đúng 1
Bình luận (0)