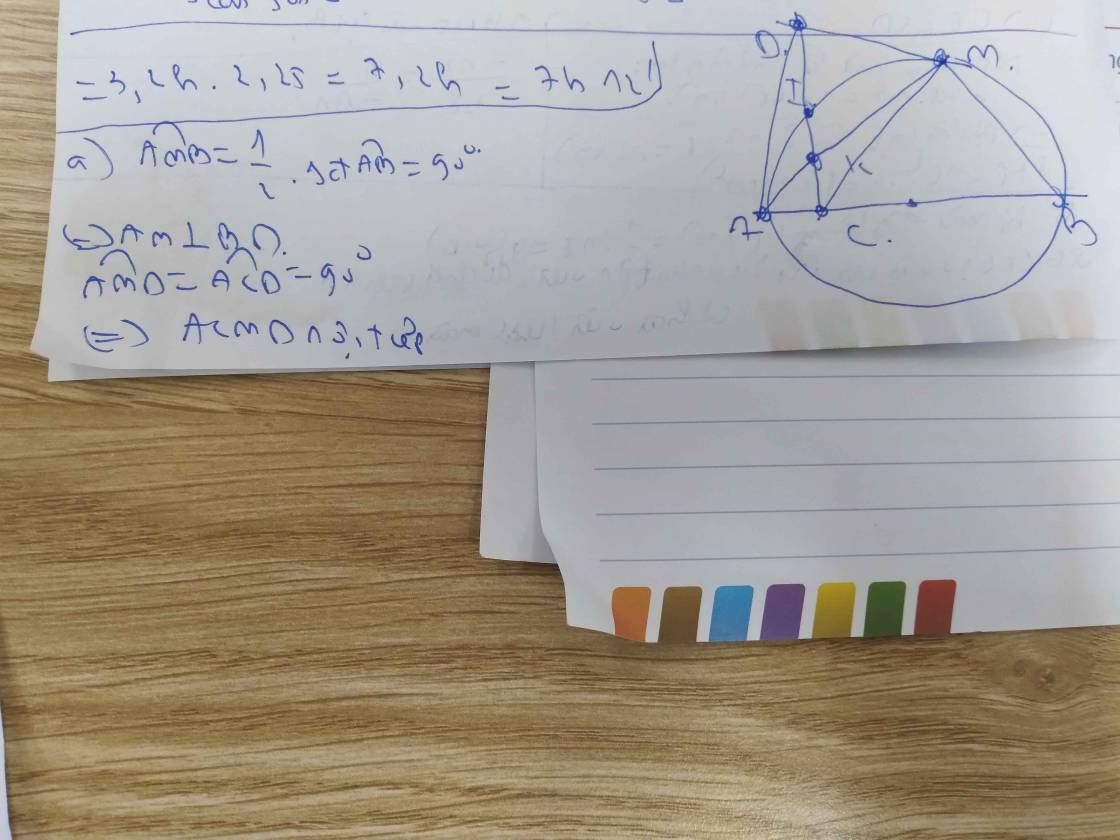
Câu 4. Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I . K là một điểm bất kì nằm trên đoạn thẳng CI , tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D . Chứng minh: 1) ACMD là tứ giác nội tiếp đường tròn. 2) ΔΑΒΟ đồng dạng ΔMBC

Những câu hỏi liên quan
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :
a) Các tứ giác : ACMD ; BCKM nội tiếp đường tròn
b) CK.CD = CA.CB
c) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CDCA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CD=CA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh: 1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn. 2) CK.CD CA.CB 3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn.
2) CK.CD = CA.CB
3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK
Đúng 1
Bình luận (0)
Giải hộ mình bài này nhé. Mình cần RẤT GẤP!!!!!!! : Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh: a) Tứ giác ACMD, BCKM nội tiếp đường tròn. b) CK.CDCA.CB c) Gọi giao điểm của AD và nửa đường tròn (O) là N. Chứng minh B,K,N thẳng hàng. d) Tâm đường tròn ngoại tiếp tam giác AKD...
Đọc tiếp
Giải hộ mình bài này nhé. Mình cần RẤT GẤP!!!!!!! : Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh: a) Tứ giác ACMD, BCKM nội tiếp đường tròn. b) CK.CD=CA.CB c) Gọi giao điểm của AD và nửa đường tròn (O) là N. Chứng minh B,K,N thẳng hàng. d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI.
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Vi NN nằm trên (O)(O) nên ˆNAB=90∘NAB^=90∘(1) ⇒NB⊥DA⇒NB⊥DA. Mà DC⊥AB,AM⊥DBDC⊥AB,AM⊥DB ⇒K⇒K Là trực tâm tam giác DABDAB suy ra BK⊥ADBK⊥AD (2). Từ (1) và (2) suy ra B,N,KB,N,K thẳng hàng
cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng
Đọc tiếp
cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd = ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng
a) Xét (O) có
ΔAMB nội tiếp đường tròn(A,M,B\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
\(\Leftrightarrow AM\perp MB\) tại M
\(\Leftrightarrow AM\perp BD\) tại M
\(\Leftrightarrow\widehat{AMD}=90^0\)
Xét tứ giác ADMC có
\(\widehat{AMD}=\widehat{ACD}\left(=90^0\right)\)
\(\widehat{AMD}\) và \(\widehat{ACD}\) là hai góc cùng nhìn cạnh AD
Do đó: ADMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A đường thẳng vuông góc với AB cắt nửa đường tròn trên tại I . K là một điểm bàng kỳ nằm trên đoạn thẳng CI ( K khác C và I ), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D.a, chứng minh : các tứ giác BCKM, ACMD nội tiếp đường tròn.b, chứng minh: ∆ABD~∆MBCc, chứng minh tâm đường tâm đường tròn ngoại tiếp tam giác ABC D nằm trên một đường thẳng tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố địn...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A đường thẳng vuông góc với AB cắt nửa đường tròn trên tại I . K là một điểm bàng kỳ nằm trên đoạn thẳng CI ( K khác C và I ), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D.
a, chứng minh : các tứ giác BCKM, ACMD nội tiếp đường tròn.
b, chứng minh: ∆ABD~∆MBC
c, chứng minh tâm đường tâm đường tròn ngoại tiếp tam giác ABC D nằm trên một đường thẳng tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định Khi K di động trên đoạn thẳn
Cho nữa đường tròn (O) đường kính AB. C là 1 điểm nằm giữa O,A . Đường vuông góc với AB tại C cắt nữa đường tròn tại I. K là một điểm bất kì nằm trên đoạn CI ( K # C và I ) .Tia AK cắt nữa đường tròn (O) tại M . Tia BM cắt tia CI tại D
a) Chứng minh các tứ giác ACMD,BCKM nội tiếp đường tròn
b) CK.CDCA.CB
C) gọi N là giao điểm của AD với đường tròn (O) . Chứng minh B,K,L thẳng hàng
d) tâm đường tròn ngoại tiếp ∆AKD nằm trên 1 đường thẳng cố định khi K di động trên đoạn CI
Đọc tiếp
Cho nữa đường tròn (O) đường kính AB. C là 1 điểm nằm giữa O,A . Đường vuông góc với AB tại C cắt nữa đường tròn tại I. K là một điểm bất kì nằm trên đoạn CI ( K # C và I ) .Tia AK cắt nữa đường tròn (O) tại M . Tia BM cắt tia CI tại D a) Chứng minh các tứ giác ACMD,BCKM nội tiếp đường tròn b) CK.CD=CA.CB C) gọi N là giao điểm của AD với đường tròn (O) . Chứng minh B,K,L thẳng hàng d) tâm đường tròn ngoại tiếp ∆AKD nằm trên 1 đường thẳng cố định khi K di động trên đoạn CI
a: góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc BMK+góc BCK=180 độ
=>BMKC nội tiếp
b: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/BC
=>CA*CB=CD*CK
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB = 2R. C là trung điểm của đoạn OA, đường thẳng Cx vuông góc với AB, Cx cắt nửa đường tròn ( O ) tại I. K là 1 điểm bất kì nằm trên đoạn CI ( K khác C, K khác I ), tia AK cắt nửa đường tròn tại M.
Tính diện tích tam giác ABD khi K là trung điểm của đoạn thẳng CI?
Ơ , em tưởng chị " ko cần bít " cơ mà ?
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O,R) đường kính AB . Gọi C là trung điểm của đoạn AO . Một đường thẳng a vuông góc với AB tại C cắt nửa đường tròn (O) tại I . Trên đoạn CI kay điểm k bất kì (K không trùng với C và I ). Tia AK cắt nửa đường tròn (O) tại M, tiếp tuyến của nửa đường tròn (O) tại M cắt đường thẳng a tại N , tia BM cắt đường thẳng a tại Da) Chứng minh rằng tam giác MNK cânb) Chứng minh rằng khi K thay đổi trên đoạn thẳng CI thì tâm đường tròn ngoại tiếp tam giác AKD luôn thuộc một đường thẳng cố...
Đọc tiếp
Cho nửa đường tròn (O,R) đường kính AB . Gọi C là trung điểm của đoạn AO . Một đường thẳng a vuông góc với AB tại C cắt nửa đường tròn (O) tại I . Trên đoạn CI kay điểm k bất kì (K không trùng với C và I ). Tia AK cắt nửa đường tròn (O) tại M, tiếp tuyến của nửa đường tròn (O) tại M cắt đường thẳng a tại N , tia BM cắt đường thẳng a tại D
a) Chứng minh rằng tam giác MNK cân
b) Chứng minh rằng khi K thay đổi trên đoạn thẳng CI thì tâm đường tròn ngoại tiếp tam giác AKD luôn thuộc một đường thẳng cố định