Tìm a và b sao cho hệ phương trình \(\left\{ \begin{array}{l}ax + by = 1\\ax + \left( {b - 2} \right)y = 3\end{array} \right.\) có nghiệm là \(\left( {1; - 2} \right).\)

Những câu hỏi liên quan
Cho hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x - y < 3\left( 1 \right)\\x + 2y > - 2\left( 2 \right)\end{array} \right.\)
a) Mỗi bát phương trình (1) và (2) có là bất phương trình bậc nhất hai ẩn không?
b) Chỉ ra một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên.
a) Hai bất phương trình bài cho là bất phương trình bậc nhất hai ẩn.
b) (1; 1) là một nghiệm chung của hai BPT (1) và (2) vì:
Thay x=1;y=1 vào (1) ta được: 1-1<3 (Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2 (Luôn đúng)
Đúng 0
Bình luận (0)
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
a) \(\left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.\)
c) \(\left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.\)
d) \(\left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right.\)
a) Hệ \(\left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.\) gồm hai bất phương trình bậc nhất hai ẩn là \(x < 0\) và \(y \ge 0\)
=> Hệ trên là hệ bất phương trình bậc nhất hai ẩn.
b) Hệ \(\left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.\) không là hệ bất phương trình bậc nhất hai ẩn vì \(x + {y^2} < 0\) không là bất phương trình bậc nhất hai ẩn (chứa \({y^2}\))
c) Hệ \(\left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.\) không là hệ bất phương trình bậc nhất hai ẩn vì \(x + y + z < 0\) có 3 ẩn không là bất phương trình bậc nhất hai ẩn.
d) Ta có:
\(\left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x + y < 9\\16x + 3y < 1\end{array} \right.\)
Đây là hệ bất phương trình bậc nhất hai ẩn và gồm hai bất phương trình bậc nhất hai ẩn là \( - 2x + y < 9\) và \(16x + 3y < 1\)
Đúng 0
Bình luận (0)
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\)
B. \(\left\{ \begin{array}{l}3x + {y^3} < 0\\x + y > 3\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x + 2y < 0\\{y^2} + 3 < 0\end{array} \right.\)
D. \(\left\{ \begin{array}{l} - {x^3} + y < 4\\x + 2y < 1\end{array} \right.\)
Ta thấy hệ \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn với các bất phương trình bậc nhất hai ẩn là \(x - y < 0;2y \ge 0\).
=> Chọn A.
Đáp án B loại vì \(3x + {y^3} < 0\) chứa \(y^3\).
Đáp án C loại vì \({y^2} + 3 < 0\) chứa \(y^2\).
Đáp án D loại vì \( - {x^3} + y < 4\) chứa \(x^3\).
Đúng 1
Bình luận (0)
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:
a) \(\left\{ \begin{array}{l}x + y - 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\)
c) \(\left\{ \begin{array}{l}x \ge 1\\x \le 4\\x + y - 5 \le 0\\y \ge 0\end{array} \right.\)
Tham khảo:
a) Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
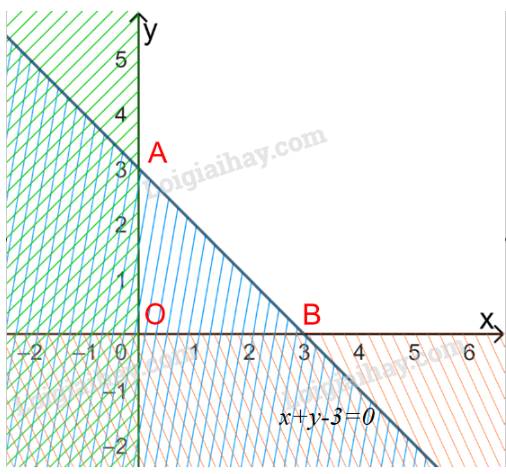
Miền không gạch chéo (bao gồm cạnh AB, tia Ay, Bx) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
b) Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
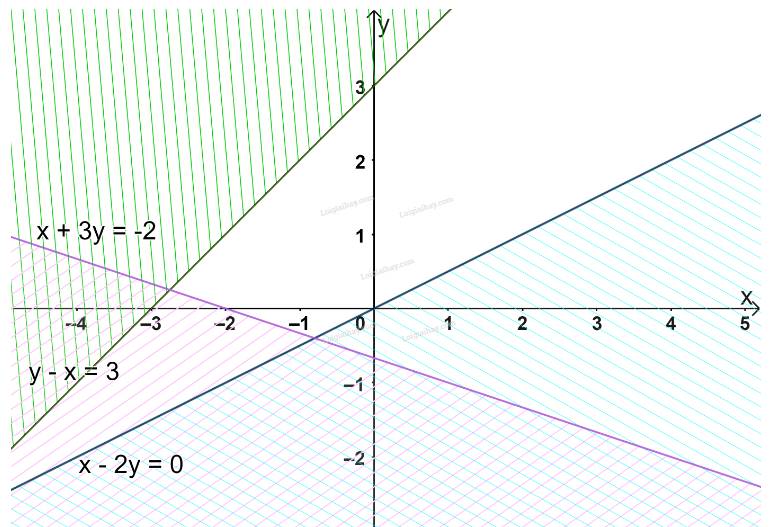
Miền không gạch chéo (không bao gồm cạnh, các bờ) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
c) Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
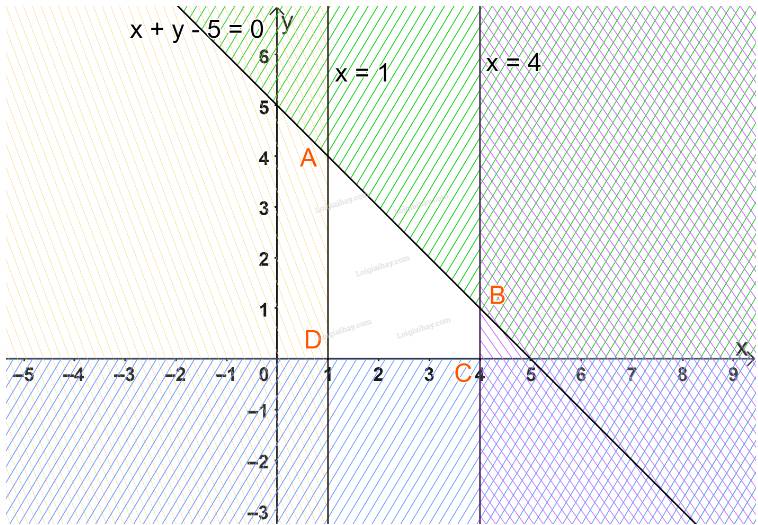
Miền không gạch chéo (miền tứ giác ABCD, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Đúng 0
Bình luận (0)
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?a) left{ begin{array}{l}x + y le 2x ge - 3y ge - 1end{array} right.b) left{ begin{array}{l}y le xx le 0y ge - 3end{array} right.c) left{ begin{array}{l}y ge - x + 1x le 2y le 1end{array} right.
Đọc tiếp
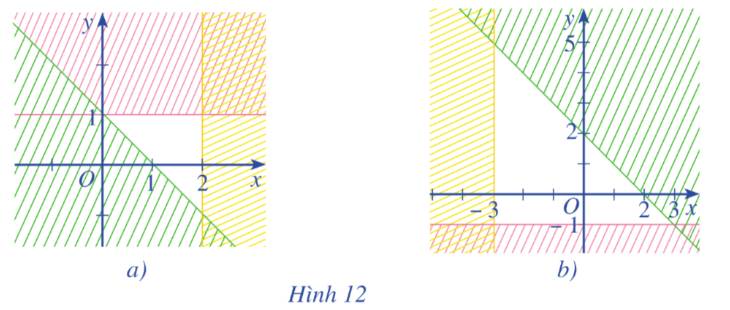
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
a) \(\left\{ \begin{array}{l}x + y \le 2\\x \ge - 3\\y \ge - 1\end{array} \right.\)
b) \(\left\{ \begin{array}{l}y \le x\\x \le 0\\y \ge - 3\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y \ge - x + 1\\x \le 2\\y \le 1\end{array} \right.\)
Hình 12a
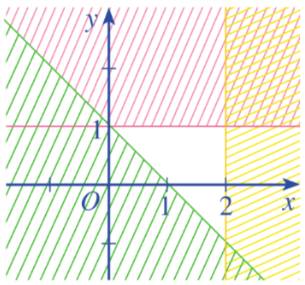
Ta thấy các đường thẳng trên hình là \(y = 1;x = 2;y = - x + 1\)
Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.
Hình 12b.
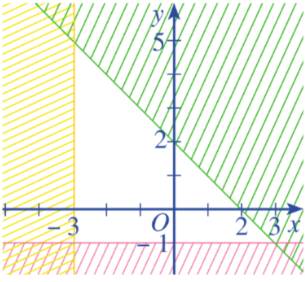
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = - 2\)
Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp
Đúng 0
Bình luận (0)
Kiểm tra xem mỗi cặp số (x;y) đã cho có là nghiệm của hệ bất phương trình tương ứng không.
a) \(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) \(\left( {0;2} \right),\left( {1;0} \right)\)
b) \(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) \(\left( { - 1; - 3} \right),\left( {0; - 3} \right)\)
a) Thay \(x = 0,y = 2\) vào hệ \(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}3.0 + 2.2 \ge - 6\\0 + 4.2 > 4\end{array} \right.\) (Đúng)
Thay \(x = 1,y = 0\) vào hệ \(\left\{ \begin{array}{l}3x + 2y \ge - 6\\x + 4y > 4\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}3.1 + 2.0 \ge - 6\\1 + 4.0 > 4\left( {Sai} \right)\end{array} \right.\)
Vậy \(\left( {0;2} \right)\) là nghiệm của hệ còn \(\left( {1;0} \right)\) không là nghiệm.
b) Thay \(x = - 1,y = - 3\) vào hệ \(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}4.\left( { - 1} \right) + \left( { - 3} \right) \le - 3\\ - 3\left( { - 1} \right) + 5.\left( { - 3} \right) \ge - 12\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 7 \le - 3\\ - 12 \ge - 12\end{array} \right.\) (Đúng)
Thay \(x = 0,y = - 3\) vào hệ \(\left\{ \begin{array}{l}4x + y \le - 3\\ - 3x + 5y \ge - 12\end{array} \right.\) ta được:
\(\left\{ \begin{array}{l}4.0 + \left( { - 3} \right) \le - 3\\ - 3.0 + 5.\left( { - 3} \right) \ge - 12\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 3 \le - 3\\ - 15 \ge - 12\left( {Sai} \right)\end{array} \right.\)
Vậy \(\left( { - 1; - 3} \right)\) là nghiệm của hệ còn \(\left( {0; - 3} \right)\) không là nghiệm.
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:
a) \(\left\{ \begin{array}{l}y - x < - 1\\x > 0\\y < 0\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 4\end{array} \right.\)
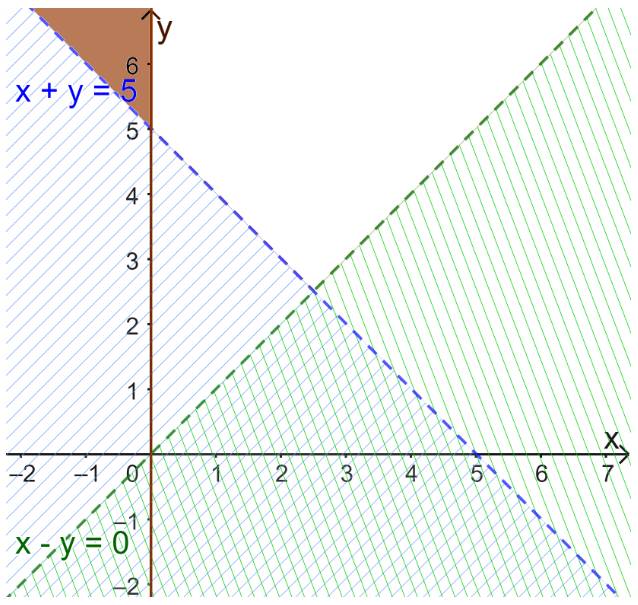
c) \(\left\{ \begin{array}{l}x \ge 0\\x + y > 5\\x - y < 0\end{array} \right.\)
a)
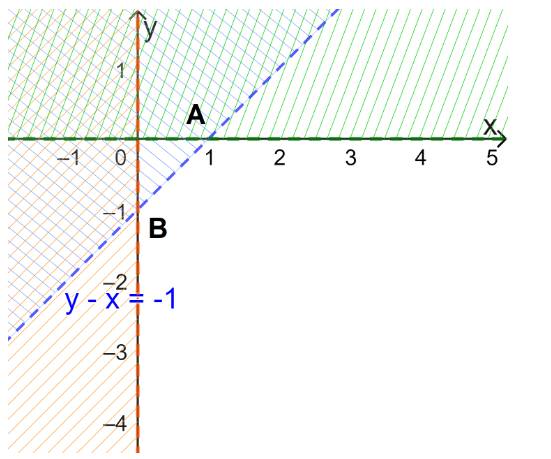
Xác định miền nghiệm của BPT \(y - x < - 1\)
+ Vẽ đường thẳng d: \(y-x= - 1\) đi qua A(1;0) và B(0;-1)
+ Vì \(0-0= 0 > - 1\) nên tọa độ điểm O(0;0) không thỏa mãn BPT \(y - x < - 1\)
Do đó, miền nghiệm của BPT \(y - x < - 1\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Miền nghiệm của BPT \(x > 0\) là nửa mặt phẳng bên phải Oy (không kể trục Oy).
Miền nghiệm của BPT \(y < 0\) là nửa mặt phẳng dưới Ox (không kể trục Ox).
Khi đó miền nghiệm của hệ bất phương trình đã cho là miền không gạch (Không kể đoạn thẳng AB và các trục tọa độ).
b)
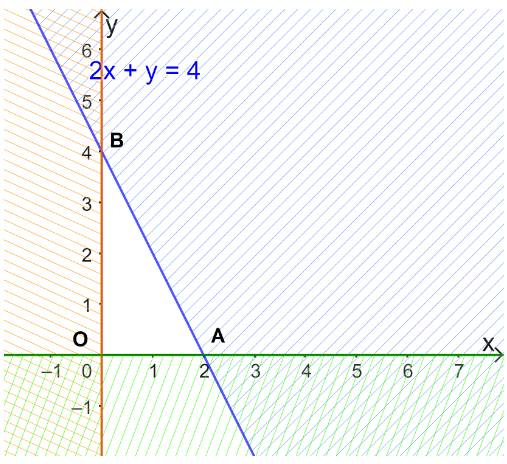
Miền nghiệm của BPT \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0) (kể cả trục Oy).
Miền nghiệm của BPT \(y \ge 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) (kể cả trục Ox).
Xác định miền nghiệm của bất phương trình \(2x + y \le 4\)
+ Vẽ đường thẳng d: \(2x + y = 4\) đi qua A(2;0) và B(0;4)
+ Vì \(2.0 + 0 = 0 < 4\) nên tọa độ điểm O(0;0) thỏa mãn BPT \(2x + y \le 4\)
Do đó, miền nghiệm của bất phương trình \(2x + y \le 4\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (kể cả các đoạn thẳng OA, OB, AB).
c)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bên phải Oy (kể cả trục Oy).
Xác định miền nghiệm của bất phương trình \(x + y > 5\)
+ Vẽ đường thẳng d: \(x + y = 5\)
+ Vì \(0 + 0 = 0 < 5\) nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình \(x + y > 5\).
Do đó, miền nghiệm của BPT \(x + y > 5\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Xác định miền nghiệm của bất phương trình \(x - y < 0\)
+ Vẽ đường thẳng d: \(x - y = 0\)
+ Vì \(1 - 0 = 1 > 0\) nên tọa độ điểm (1;0) không thỏa mãn bất phương trình \(x - y < 0\)
Do đó, miền nghiệm của bất phương trình \(x - y < 0\) là nửa mặt phẳng bờ d’ không chứa điểm (1;0).
Vậy miền nghiệm của hệ bất phương trình đã cho là miền màu trắng (không kể d và d’)
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của hệ bất phương trình:
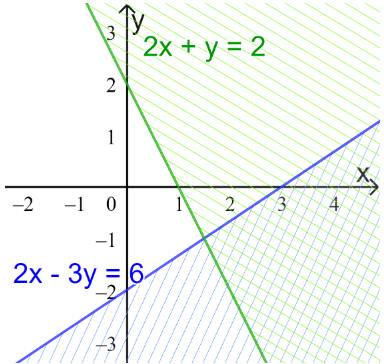
a) \(\left\{ \begin{array}{l}2x - 3y < 6\\2x + y < 2\end{array} \right.\)
b) \(\left\{ \begin{array}{l}4x + 10y \le 20\\x - y \le 4\\x \ge - 2\end{array} \right.\)
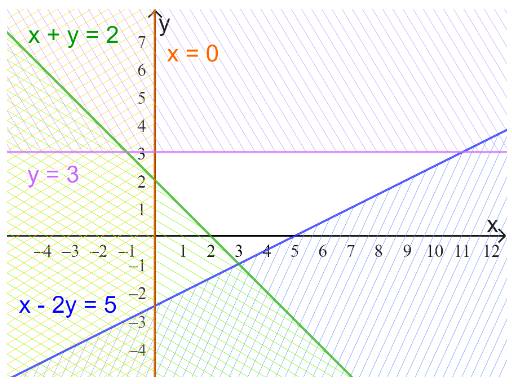
c) \(\left\{ \begin{array}{l}x - 2y \le 5\\x + y \ge 2\\x \ge 0\\y \le 3\end{array} \right.\)
a) Vẽ các đường thẳng \(2x - 3y = 6;2x + y = 2\) (nét đứt)
Thay tọa độ điểm O vào các bất phương trình trong hệ.
Ta thấy: 2.0-3.0
=> O thuộc miền nghiệm của cả 2 bất phương trình
Miền nghiệm:
b)
Vẽ các đường thẳng
\(4x + 10y \le 20 \Leftrightarrow y = - \frac{2}{5}x + 2\) (nét liền)
\(x - y = 4 \Leftrightarrow y = x - 4\)(nét liền)
\(x = - 2\)(nét liền)
Thay tọa độ điểm O vào các bất phương trình trong hệ.
Ta thấy: 4.0+10.0-2
=> O thuộc miền nghiệm của cả 3 bất phương trình
Miền nghiệm:

c)
Vẽ các đường thẳng
\(x - 2y = 5 \Leftrightarrow y = \frac{1}{2}x - 5\) (nét liền)
\(x + y = 2 \Leftrightarrow y = - x + 2\)(nét liền)
\(y = 3\)(nét liền)
Và trục Oy
Thay tọa độ O vào bất phương trình \(x - 2y \le 5\)
=> O thuộc miền nghiệm của bất phương trình trên.
Thay tọa độ O vào \(x + y \ge 2\)
=> O không thuộc miền nghiệm của bất phương trình trên
Lấy phần bên phải trục Oy và bên dưới đường thẳng y=3
Miền nghiệm:
Đúng 0
Bình luận (0)
Cho hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}x + y > 2\\x - y \le 1\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
A. (1;1)
B. (2;0)
C. (3;2)
D. (3;-2)
(1;1) không thuộc miền nghiệm vì 1+1=2>2 (Vô lý) => Loại A
(2;0) không thuộc miền nghiệm vì 2+0=2>2 (Vô lý) => Loại B
(3;2) thuộc miền nghiệm vì: 3+2 =5 > 2 (đúng) và \(3 - 2 = 1 \ge 1\) (đúng)
(3;-2) không thuộc miền nghiệm vì 3+ (-2)=1>2 (Vô lý) => Loại D
Chọn C.
Đúng 0
Bình luận (0)
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < - 3\\2y \ge - 4\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?
A. (0;0)
B. (-2;1)
C. (3;-1)
D. (-3;1)
Thay tọa độ điểm (0;0) vào ta được: \(\left\{ \begin{array}{l}0 - 0 < - 3\left( {ktm} \right)\\2.0 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại A
Thay tọa độ điểm (-2;1) vào ta được: \(\left\{ \begin{array}{l} - 2 - 1 < - 3\left( {ktm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại B.
Thay tọa độ điểm (3;-1) vào ta được: \(\left\{ \begin{array}{l}3 - \left( { - 1} \right) < - 3\left( {ktm} \right)\\2.\left( { - 1} \right) \ge - 4\left( {tm} \right)\end{array} \right.\)
Loại C
Thay tọa độ điểm (-3;1) vào ta được: \(\left\{ \begin{array}{l} - 3 - 1 < - 3\left( {tm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
Chọn D.
Đúng 1
Bình luận (0)



