Cho\(\Delta ABC\)vuông ở A có các cạnh a, b, c. Đường trong (O) nội tiếp tam \(\Delta ABC\)tiếp xúc BC, CA, AB ở M, N, P. Hỏi tứ giác ANOP là hình gì và chứng minh\(\Delta ABC=MB.MC\)

Những câu hỏi liên quan
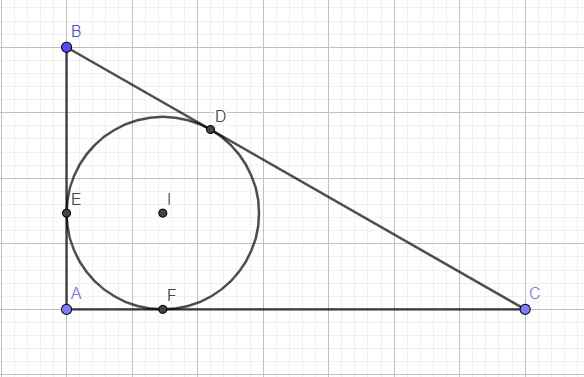
Cho tam giác ABC vuông tại A. Đường tròn tâm (I) nội tiếp tam giác ABC tiếp xúc với cạnh BC tại D. Chứng minh rằng: S\(\Delta ABC\) = BD.DC
Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)
Đúng 1
Bình luận (0)
Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$, điểm $M$ thuộc cung $BC$ không chứa $A$. Vẽ $MH$ vuông góc với $AB$ tại $H$ và $MK$ vuông góc với $AC$ ở $K$.
a/ Chứng minh tứ giác $AHMK$ nội tiếp.
b/ Chứng minh \(\Delta MHK \backsim\Delta MBC\).
c/ Giả sử $HK$ cắt $BC$ tại $G$. Chứng minh \(MG\perp BC\).
ko biết dâu nha
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có AC>AB. Gọi I là tâm đường tròn nội tiếp tam giác ABC, các tiếp điểm của đường tròn nội tiếp với các cạnh AB,BC,CA lần lượt tại M,N,P.
a) Chứng minh tứ giác AMIP là hình vuông
b) Đường thẳng AI cắt PN tại D. Chứng minh 5 điểm M,B,N,O,I nằm trên một đường tròn
cho đường tròn tam O nội tiếp tam giác ABC (ABAC) tiếp xúc với các cạnh BC,CA,AB tương ứng tại D,E,F.Đườn tròn tâm O bàng tiếp trong góc BAC của tam giác ABC tiếp xúc với cạnh BC và phần kéo dài của các cạnh AB,AC tương ứng tại các điểm P,M,N.a)chứng minh BPCDb)trên đường thawngrMN lấy các điển I,K sao cho CK//AB,BI//AC. chứng minh các tứ giác BICE,BKCF là hình thang cânc)gọi (S) là đường tròn đi qua ba điểm I,K,P.chứng minh(S) tiếp xúc với các đường thẳng BC,BI,CK
Đọc tiếp
cho đường tròn tam O nội tiếp tam giác ABC (AB<AC) tiếp xúc với các cạnh BC,CA,AB tương ứng tại D,E,F.Đườn tròn tâm O' bàng tiếp trong góc BAC của tam giác ABC tiếp xúc với cạnh BC và phần kéo dài của các cạnh AB,AC tương ứng tại các điểm P,M,N.
a)chứng minh BP=CD
b)trên đường thawngrMN lấy các điển I,K sao cho CK//AB,BI//AC. chứng minh các tứ giác BICE,BKCF là hình thang cân
c)gọi (S) là đường tròn đi qua ba điểm I,K,P.chứng minh(S) tiếp xúc với các đường thẳng BC,BI,CK
Cho đường tròn (I) nội tiếp tam giác ABC, tiếp xúc với các cạnh AB, CA tại D, E. Các tia CI, BI lần lượt cắt DE tại M, N. Chứng minh:
a) \(\Delta BDN\)đồng dạng \(\Delta BIC\)
b) \(\Delta BDN\)đồng dạng \(\Delta MEC\)
Cho Delta ABCnội tiếp đường tròn (O), các tia phân giác của các góc widehat{ABC}và widehat{ACB} cắt nhau tại I và cắt đường tròn lần lượt tại các điểm D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh rằng:a) các Delta AMN,Delta EAI,Delta DAIlà những tam giác cânb) tứ giác AMIN là hình thoi
Đọc tiếp
Cho \(\Delta ABC\)nội tiếp đường tròn (O), các tia phân giác của các góc \(\widehat{ABC}\)và \(\widehat{ACB}\) cắt nhau tại I và cắt đường tròn lần lượt tại các điểm D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh rằng:
a) các \(\Delta AMN,\Delta EAI,\Delta DAI\)là những tam giác cân
b) tứ giác AMIN là hình thoi
Cho tam giác ABC vuông ở A, AC=6, $\hat{C}=30^0$. Vẽ (O) đường kính AC cắt BC tại D, dây DE vuông góc AC tại H. Qua B vẽ tiếp tuyến của (O) tại M.
a. Tính BC và chứng minh tam giác CDE đều.
b. Chứng minh: $\Delta BDM$ ~ $\Delta BMC$.
c. Gọi K là hình chiếu của H trên EC và I là trung điểm HK. Chứng minh: DK vuông góc CI.
Cho ΔABC nhọn nội tiếp đường tròn (O) .Hai đường cao BD và CE cắt nhau tại H .Tia AO cắt đường tròn ở M và cắt DE ở I. Chứng minh:
a) Tứ giác AEHD và BCDE là tứ giác nội tiếp
b) ΔADE và ΔABC đồng dạng
c) Tứ giác DIMC là tứ giác nội tiếp
d) AM⊥ED
Cho đường tròn (O) đường kính AB. Gọi d là tiếp tuyến tại A. Lấy C tùy ý thuộc (O) sao cho CA CB, tia BC cắt d ở D.
a) Chứng minh: Delta ABCsimDelta DAC
b) Vẽ tiếp tuyến của (O) tại C cắt d tại E. Chứng minh: tứ giác OCEA nội tiếp.
c) Gọi G là điểm chính giữa của cung nhỏ AC. Chứng minh: G là tâm đường tròn nội tiếp Delta ACE
d) Tia BG cắt d tại H. CHứng mnih: tứ giác CGHD nội tiếp
Đọc tiếp
Cho đường tròn (O) đường kính AB. Gọi d là tiếp tuyến tại A. Lấy C tùy ý thuộc (O) sao cho CA > CB, tia BC cắt d ở D.
a) Chứng minh: \(\Delta ABC\sim\Delta DAC\)
b) Vẽ tiếp tuyến của (O) tại C cắt d tại E. Chứng minh: tứ giác OCEA nội tiếp.
c) Gọi G là điểm chính giữa của cung nhỏ AC. Chứng minh: G là tâm đường tròn nội tiếp \(\Delta ACE\)
d) Tia BG cắt d tại H. CHứng mnih: tứ giác CGHD nội tiếp