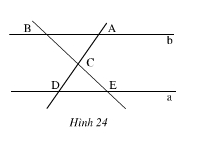
Cho hình 24 (SGK trang 95) a // b. Hãy nêu các cặp góc bằng nhau của hai tam giác CAB và CDE

Những câu hỏi liên quan
Cho hình 24 (a // b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE.
Vì a // b nên hai tam giác CAB và CDE có:
Cho hình 24 (a // b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE.
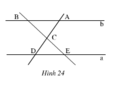
Vì a // b nên hai tam giác CAB và CDE có:

Đúng 0
Bình luận (0)
Cho hình 24 (a //b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE ?
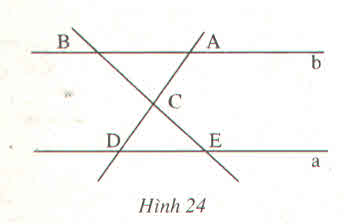
Ta có:
^ECD = ^ACB (2 góc đối đỉnh).
Vì a // b nên:
^ABC = ^CED và ^CDE = BAC (2 góc so le trong)
Vậy các cặp góc bằng nhau của 2 tam giác CAB và CDE là: ^ACB = ^ECD; ^BAC = ^CDE; ^ABC = ^CED.
Đúng 0
Bình luận (0)

cho hình 24 ( a // b ) . hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE.
~~PLEASE~~
Cho hình 24 (a // b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE.
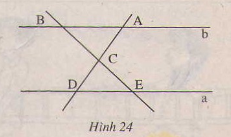
Góc ACB= góc DCE
Góc CAB= góc CDE
Góc CBA= góc CED
Đúng 0
Bình luận (0)
góc CAB = góc CDE
góc CBA = góc CED
góc ACB = góc DCE
chúc bạn học tốt![]()
Đúng 0
Bình luận (0)
ta có hình vẽ :

A = D ( SO LE TRONG )
B = E ( SO LE TRONG )
C1 = C2 ( ĐỐI ĐỈNH )
~~~ GOOD LUCK TO YOU ! ~~~
Đúng 0
Bình luận (0)
1 . Cho hình vẽ : Biết a // b . Hãy nêu tên các cặp góc băng nhau của 2 tam giác CAB và CDE

cde = CBA =3 ĐIỂM
BAC=DEC = 3 ĐIỂM
DCE =BCA=4ĐIỂM
Đúng 0
Bình luận (0)
BAC = DCE (đối đỉnh)
CAB = CDE (so le trong)
ABC = CED (so le trong)
Đúng 1
Bình luận (0)
cho tam giác abc có góc b =130 độ,.Trên cạnh AC lấy hai điểm D và E sao cho <ABD và <CDE là 2 góc phụ nhau a) Trên hình vẽ có tất cả bao nhiêu hình tam giác,hãy kể tên? b) Kể tên các cặp góc kề bù c) Tính số đo góc DBE Các bạn vẽ hình cho mình với nhé
cho tam giác ABC có ia phân giác trong của góc CAB và góc CBA cắt nhau tại D . Các tia phân giác ngoài ở đỉnh A và B cắt nhau ở E . Chứng minh CDE thảng hàng
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
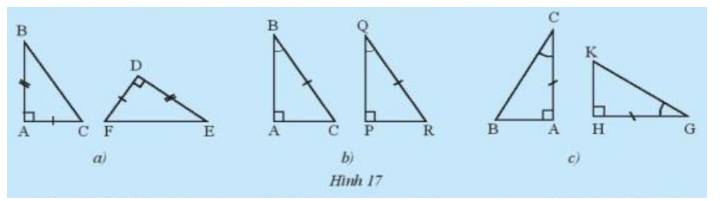
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)
Đúng 0
Bình luận (0)