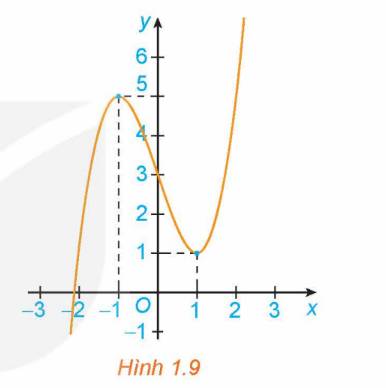
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ (dưới bình luận). Tìm tất cả các giá trị của tham số m để hàm số y= \(\left|f^2\left(x\right)-4f\left(x\right)+m\right|\) có 7 điểm cực trị (giải theo phương pháp ghép trục)
Cho hàm số y=f(x) liên tục trên K có đạo hàm f'(x) Đồ thị của hàm số f'(x) như hình vẽ bên.
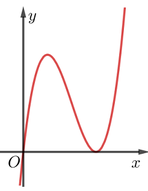
Tìm số điểm cực trị của đồ thị hàm số f(x)?
A. 3
B. 1
C. 0
D. 2
Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
Cho đồ thị hàm số y = f(x) có đồ thị đạo hàm như hình vẽ. Số điểm cực trị của đồ thị hàm số y = f ( x 3 ) là:
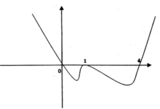
A. 0
B. 1
C. 2
D. 3
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Cho hàm số bậc ba \(y=f\left(x\right)\) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số \(m\in\left[0;20\right]\) để hàm số \(g\left(x\right)=\left|f^2\left(x\right)-2f\left(x\right)-m\right|\) có 9 điểm cực trị?
A. 8 B. 9 C. 10 D. 11
Giải chi tiết cho mình bài này với ạ, mình cảm ơn nhiều♥

Đặt \(h\left(x\right)=f^2\left(x\right)-2f\left(x\right)-m\Rightarrow h'\left(x\right)=2f'\left(x\right)\left[f\left(x\right)-1\right]\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(x\right)=1\end{matrix}\right.\)
Từ đồ thị ta thấy \(f'\left(x\right)=0\) có 2 nghiệm (do \(f\left(x\right)\) có 2 cực trị) và \(y=1\) cắt \(y=f\left(x\right)\) tại 3 điểm
\(\Rightarrow h'\left(x\right)=0\) có 5 nghiệm
\(\Rightarrow\) Hàm \(g\left(x\right)\) có 9 cực trị khi \(f^2\left(x\right)-2f\left(x\right)-m=0\) có 4 nghiệm không trùng với nghiệm của \(h'\left(x\right)=0\)
TH1: \(m=0\Rightarrow f^2\left(x\right)-2f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f\left(x\right)=0\\f\left(x\right)=2\end{matrix}\right.\)
\(f\left(x\right)=0\) có 2 nghiệm, trong đó 1 nghiệm trùng với \(f'\left(x\right)=0\) nên chỉ tính 1 nghiệm, \(f\left(x\right)=2\) có 3 nghiệm \(\Rightarrow f^2\left(x\right)-2f\left(x\right)=0\) có 4 nghiệm ko trùng \(h'\left(x\right)=0\) (thỏa mãn)
TH2: \(m>0\), đặt \(k=f\left(x\right)\Rightarrow k^2-2k-m=0\) (1) luôn có 2 nghiệm pb trái dấu \(k_1< 0< k_2\) do \(c=-m< 0\)
Từ đồ thị ta thấy \(f\left(x\right)=k_1\) luôn có đúng 1 nghiệm
Do đó, \(f\left(x\right)=k_2\) phải có 3 nghiệm phân biệt đồng thời \(k_2\ne1\) \(\Rightarrow\left\{{}\begin{matrix}0< k_2< 4\\k_2\ne1\end{matrix}\right.\)
(\(k_2\) là nghiệm dương của (1) nên \(k_2=1+\sqrt{m+1}\))
\(\Rightarrow\left\{{}\begin{matrix}0< 1+\sqrt{m+1}< 4\\1+\sqrt{m+1}\ne1\end{matrix}\right.\) \(\Rightarrow m< 8\Rightarrow m=\left\{1;2;3;4;5;6;7\right\}\)
Kết hợp lại ta được \(m=\left\{0;1;...;7\right\}\) có 8 giá trị nguyên của m thỏa mãn
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
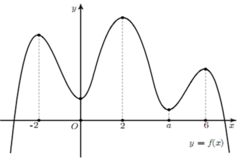
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
Cho hàm số y = f(x). Hàm số y = f ' (x) có đồ thị như hình bên.
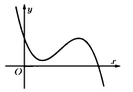
Tìm số điểm cực trị của hàm số y = f(x).
A. 3
B. 1
C. 0
D. 2
Đáp án B.
f ' (x) đổi dấu 1 lần, suy ra hàm số y = f(x) có 1 điểm cực trị.
Cho hàm sốy=f(x). Hàm số y=f’(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y=f(x)

A. 0
B. 1
C. 2
D. 3
Đáp án B
Nhìn vào đồ thị hàm số ta thấy có một giá trị của x (gải sử x = a) để y’=0 và không có giá trị nào của x làm y’ không xác định. Mặt khác y' đổi dấu từ dương sang âm khi đi qua x = a do vậy x = a là một điểm cực trị của hàm số y=f(x).
Ta chọn B
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Cho hàm số y= f( x) và đồ thị hình bên là đồ thị của hàm y= f’ ( x) . Hỏi đồ thị của hàm số g ( x ) = 2 f ( x ) - x - 1 2 có tối đa bao nhiêu điểm cực trị ?

A. 6.
B. 7.
C. 8.
D. 9.
Đặt h( x) = 2f( x) – ( x-1) 2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
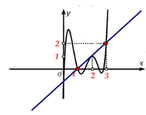
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > .0 khi f’(x) > x-1
Ta có :

Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.