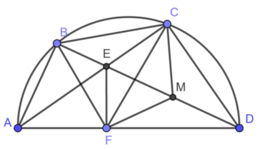
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD.Hai đường chéo AC và BD cắt nhau tại E.Kẻ EF vuông góc với AD.Gọi M là trung điểm của DE.Chứng minh:
a)Các tứ giác ABEF,DCEF nội tiếp
b)tia CA là tia phân giác của góc BCF
giup minh voii

Những câu hỏi liên quan
cho tứ giác ABCD nội tiếp đường tròn đường kính AD.hai đường chéo AC vàBD cắt nhau tại E.kẻ EF vuông góc với AD tại F.chứng minh rằng.
A)chứng minh tứ giác dcef nội tiếp được
B) chứng minh tia CA là tia phân giác của góc bcf
a) Xét đường tròn tâm O đường kính AD có \(\widehat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) hay \(\widehat{ECD}=90^o\)
Xét tứ giác DCEF có: \(\widehat{ECD}+\widehat{EFD}=90^o+90^o=180^o\)
=> DCEF là tứ giác nội tiếp
b) Do DCEF là tứ gíc nội tiếp (cmt) => \(\widehat{C_2}=\widehat{D_1}\) (cùng nhìn cạnh EF)
ABCD là tứ giác nội tiếp => \(\widehat{C_1}=\widehat{D_1}\) (cùng nhìn cạnh AB)
=> \(\widehat{C_1}=\widehat{C_2}\left(=\widehat{D_1}\right)\) => CA là tia phân giác góc BCF
Đúng 2
Bình luận (0)
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng: Các tứ giác ABEF, DCEF nội tiếp được
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc AD tại F. Gọi M là trung điểm DE. Chứng minh:
a) Các tứ giác ABEF, DCEF nội tiếp
b) CA là phân giác góc BCF
c) Tứ giác BCMF nội tiếp
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD ( F thuộc AD), CF cắt đường trong tại M. Chứng minh rằng:
a) các tứ giác ABEF;DCEF nội tiếp đường tròn.
B) tia CA là tia phân giác của góc BCF
C) BM vuông góc AD
Ta có: ˆACD=900ACD^=900 (góc nội tiếp chắn nửa đường tròn đường kính AD)
Xét tứ giác DCEF có:
ˆACD=900ACD^=900 (cm trên)
ˆEFD=900EFD^=900 (vì EF⊥ADEF⊥AD (gt))
⇒ˆACD+ˆEFD=1800⇒ACD^+EFD^=1800
=> Tứ giác DCEF là tứ giác nội tiếp đường tròn (đpcm).
b) Vì tứ giác DCEF là tứ giác nội tiếp (chứng minh câu a)
⇒ˆC1=ˆD1⇒C1^=D1^ (góc nội tiếp cùng chắn cung EF) (1)
Mà ⇒ˆC2=ˆD1⇒C2^=D1^ (góc nội tiếp cùng chắn cung AB) (2)
Từ (1) và (2) ⇒ˆC1=ˆC2⇒C1^=C2^
⇒⇒ CA là tia phân giác của ˆBCFBCF^ (đpcm)
k đúng hộ
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD , hai đường chéo AC và BD cắt nhau tại E . Vẽ EF vuông góc với AD , gọi M là trung điểm của DE. Chứng Minh rằng :
a)Các tứ giác ABEF và DCEF nội tiếp được
b) Tia CA là phân giác của góc BCF
bạn tự vẽ hình nha
a)Xét tứ giác ABEF có
góc ABE=90 độ( góc nội tiếp chắn nửa dường tròn)
và góc AFE=90 độ (EF vuông góc AD tại F)
=> góc ABE + góc AFE =180 độ
=> tứ giác ABEF nội tiếp dường tròn đường kính AE
b)Ta có : góc CBD=góc CAD ( góc nội tiếp cùng chắn cung CD của (O))
và góc CAD =góc FBD (góc nội tiếp chắn cung EF của đường tròn ngoại tiếp tứ giác ABEF)
=>góc CBD=góc FBD (=góc CAD)
=>BD là tia phân giác của góc CBF
c)Xét tứ giác CEFD có:
góc DCA=90 độ (góc nội tiếp chắn nửa đường tròn)
và góc EFD=90 độ (EF vuông góc AD tại F)
=> góc DCA+góc EFD=180 độ
=> tứ giác CEFD nội tiếp dường tròn đường kính ED)
Ta có tam giác ABE vuông tại B có dường trung tuyến BM (M là trung diểm của AE)
=>BM=1/2. AE= AM=ME =>tam giác ABM cân tại M => góc ABM= góc BAM
mà góc ABM +góc MBF+góc FBE=90 độ
và góc FBE=góc CAD (cmt)
=>góc MBF+ góc CAD+ góc BAM =90 độ
mà góc ADB+ góc CAD+góc BAM =90 độ(góc BAD=góc BAM+goc1CAD)
=>góc MBF=góc ADB
mà góc ADB = góc FCM ( góc nội tiếp cùng chắn cung EF của đường tròn ngoại tiếp tứ giác CEFD)
=>góc MBF= góc FCM (=góc ADB)
=>tứ giác BMFC nội tiếp đường tròn
#B

a) Ta có: ^ABD = 90o ( góc nội tiếp chắn cung AD ( nửa đường tròn ) )
và ^AFE = 90o ( EF vuông AD)
=> ^ABD + ^AFE = 180o
=> ABEF nội tiếp
Chứng minh tương tự với DCEF
b) ABCD nội tiếp => ^ACB = ^ADB ( cùng chắn cung AB )
DCEF nội tiếp => ^ECF = ^EDF ( cùng chắn cung EF ) => ^ACF = ^ADB
=> ^ACB = ^ACF
=> CA là phân giác ^BCF
cô ơi của em có đúng không ạ
Xem thêm câu trả lời
cho tứ giác ABCD nội tiếp nửa đường tròn, đường kính AD. hai đường chéo AC và BD cắt nhau tại E, EF vuông góc với AD tại F. cm ABeF và DCEF là các tứ giác nội tiếp
Tự vẽ hình nha ><
a) ^ABD = 900 => ^ABE = 900
EF \(\perp\)AD => ^EFA = 900
=> Tứ giác ABEF có tổng 2 góc đối = 900 nội tiếp được đường tròn
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E . Kẻ EF vuông góc AD . CMR Các tứ giác ABEF , DCEF nội tiếp .
Cho tứ giác ABCD nội tiếp nửa đưởng tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc vớI AD. Chứng minh:
a, Tứ giác ABEF, DCEF nội tiếp
b, CA là phân giác của góc BCF
c, Gọi M là trung điểm của DE, chứng minh tứ giác BCMF nội tiếp.
MỌI NGƯỜI AI BIẾT LÀM GIẢI GIÚP MÌNH PHẦN C. CẢM ƠN NHIỀU <3
cho tứ giác ABCD nội tiếp nửa đường tròn , đường kính AD. hai đường chéo AC và BD cắt nhau tại E.kẻ EF vuông góc với AD tại F. gọi M là trung điểm của DE. cm tứ giác BCMF nội tiệp
Xét $(O)$ có: $\widehat{ACD}=\widehat{ABD}=90^o$( góc nội tiếp chắn nửa đường tròn)
suy ra $\widehat{ECD}=90^o$
$\widehat{BAC}=\widehat{BDC}$ (các góc nội tiếp cùng chắn cung $BC$)
hay $\widehat{BAE}=\widehat{EDC}(1)$
Xét tứ giác $BEFA$ có: $\widehat{ABE}=\widehat{EFA}=90^o$ (do $EF AD$)
nên $\widehat{ABE}+\widehat{EFA}=180^o$
suy ra tứ giác $BEFA$ nội tiếp
suy ra $\widehat{EFB}=\widehat{BAE}(2)$ (các góc nội tiếp cùng nhắn $BE$)
Chứng minh tương tự ta có: tứ giác $ECDF$ nội tiếp nên $\widehat{EFC}=\widehat{EDC}(3)$ (các góc nội tiếp cùng chắn cung $EC$)
Từ $(1)(2)(3)$ suy ra $\widehat{EFB}+\widehat{EFC}=\widehat{BAE}+\widehat{EDC}=2.\widehat{EDC}$
hay $\widehat{BFC}=2.\widehat{EDC}$
Lại có: tam giác $ECD$ vuông tại $C$
$M$ là trung điểm $ED$
Nên $EM=MD=CM$
Suy ra tam giác $MCD$ cân tại $M$
nên $\widehat{MCD}=\widehat{MDC}$
Lại có: $\widehat{BMC}$ là góc ngoài tam giác $MCD$ nên
$\widehat{BMC}=\widehat{MCD}+\widehat{MDC}=2.\widehat{MDC}=2.\widehat{EDC}
Mà $\widehat{BFC}=2.\widehat{EDC}$
nên $\widehat{BMC}=\widehat{BFC}$
suy ra $F;M$ cùng nhìn đoạn $BC$ dưới 1 góc ko đổi
$F;M$ là 2 đỉnh liên tiếp tứ giác $BCMF$
suy ra tứ giác $BCMF$ nội tiếp (Bài toan quỹ tích cung chứa góc)
Đúng 2
Bình luận (0)
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD , hai đường chéo AC và BD cắt nhau tại E.Vẽ È vương góc với AD , gọi M là trung điểm của DE . Chứng Minh rằng :
a)Các tứ giác ABEF,DCEF nội tiếp được
b) Tia CA là phân giác của góc BCF