giaỉ phương trình

Giải phương trình

Ta đặt:
\(\sqrt{x-2009}=a\)
\(\sqrt{y-2010}=b\)
\(\sqrt{z-2011}=c\)
Với a ; b ; c >0 . Khi này , pt trở thành:
\(\dfrac{a-1}{a^2}+\dfrac{b-1}{b^2}+\dfrac{c-1}{c^2}=\dfrac{3}{4}\)
\(\Leftrightarrow\left(\dfrac{1}{4}-\dfrac{1}{a}+\dfrac{1}{a^2}\right)+\left(\dfrac{1}{4}-\dfrac{1}{b}+\dfrac{1}{b^2}\right)+\left(\dfrac{1}{4}-\dfrac{1}{c}+\dfrac{1}{c^2}\right)=0\)
\(\Leftrightarrow\left(\dfrac{1}{2}-\dfrac{1}{a}\right)^2+\left(\dfrac{1}{2}-\dfrac{1}{b}\right)^2+\left(\dfrac{1}{2}-\dfrac{1}{c}\right)^2=0\)
\(\Leftrightarrow a=b=c=2\)
Suy ra :
x = 2013
y = 2014
z = 2015
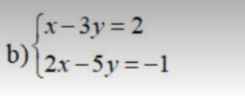 giải hệ phương trình
giải hệ phương trình
Ta có: x -3y =2
<=> 2x-6y =4 (1)
* 2x-5y= -1 (2)
Phương trình (1) -pt (2) ta có:
2x -6y -(2x-5y) =4-(-1)
<=> 2x- 6y -2x+5y =5
<=>y= -5
Thay y= -5 vào pt (2) ta có:
2.x -5.(-5) =-1
<=>2x +25 =-1
<=> 2x=-26
<=> x=-13
Giải hệ phương trình sau
\(\left\{{}\begin{matrix}x^2+y^2+6x+2y=0\\x+y+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+\left(x+8\right)^2+6x-2\left(x+8\right)=0\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+10x+24=0\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=-4\\x=-6\end{matrix}\right.\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-4\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-2\end{matrix}\right.\end{matrix}\right.\)
Kết luận: Hệ phương trình đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(-4;-4\right);\left(-6;-2\right)\right\}\)
Cho phương trình : \(^{x^2-2\left(m-2\right)x+m^2-3m+5=0}\)
a) giải phương trình với m=3
a) Thay m=3 vào phương trình, ta được:
\(x^2-2x+3^2-3\cdot3+5=0\)
\(\Leftrightarrow x^2-2x+5=0\)
\(\Leftrightarrow x^2-2x+1+4=0\)
\(\Leftrightarrow\left(x-1\right)^2+4=0\)(vô lý)
Vậy: Khi m=3 thì phương trình vô nghiệm
cho phương trình ẩn x: \(9x^2-25-k^2-2kx=0\)
a,Giải phương trình với k=0
b,Tìm các giá trị của k sao cho phương trình nhận x=-1 làm nghiệm số
thay k=0 vào pt ta được
\(9x^2-25-0^2-2.0x=0\)
=>\(9x^2-25=0\)
=>\(\left(3x-5\right)\left(3x+5\right)=0\)
=>\(3x+5=0=>x=\dfrac{-5}{3}\)
hoặc \(3x-5=0=>x=\dfrac{5}{3}\)
cho phương trình ẩn x: \(9x^2-25-k^2-2kx=0\)
a,Giải phương trình với k=0
b,Tìm các giá trị của k sao cho phương trình nhận x=-1 làm nghiệm số
Thay `k=0` vào pt ta có:
`9x^2-25-0-0=0`
`<=>9x^2=25`
`<=>x^2=25/9`
`<=>x=+-5/3`
`b)x=-1` làm nghiệm nên ta thay `x=-1` vào pt thì pt =0
`=>9.1-25-k^2-2k(-1)=0`
`<=>-16-k^2+2k=0`
`<=>k^2-2k+16=0`
`<=>(k-1)^2+15=0` vô lý
Vậy khong có giá trị của k thỏa mãn đề bài
Giải phương trình log 3 x + log 9 x + log 81 x = 7
A. x = 27
B. x = 81
C. x = 729
D. x = 243
Điều kiện : x > 0
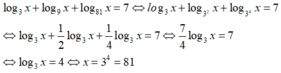
Kết hợp điều kiện, vậy x = 81.
Chọn B
Giải phương trình sau: 3 sinx + cosx = 1 cosx
A. x = k2π
B. x = π 3 + k2π
C. x = π 3 + kπ
D. x = π 6 + kπ
Giải phương trình: x + 1 2 − 1 = 0
x + 1 2 − 1 = 0 ⇔ x + 1 2 = 1 ⇔ x + 1 = 2 ⇔ x = 1
Vậy nghiệm của phương trình là x = 1.
giải bất phương trình |2x+3| ≥18