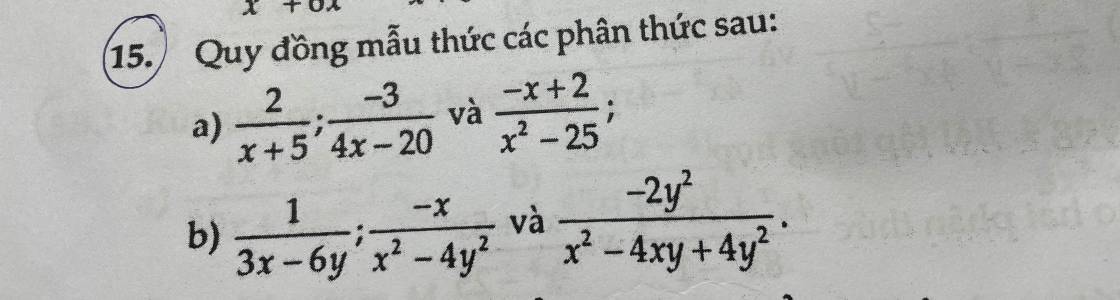 giúp nốt em ạa🥲
giúp nốt em ạa🥲

Những câu hỏi liên quan
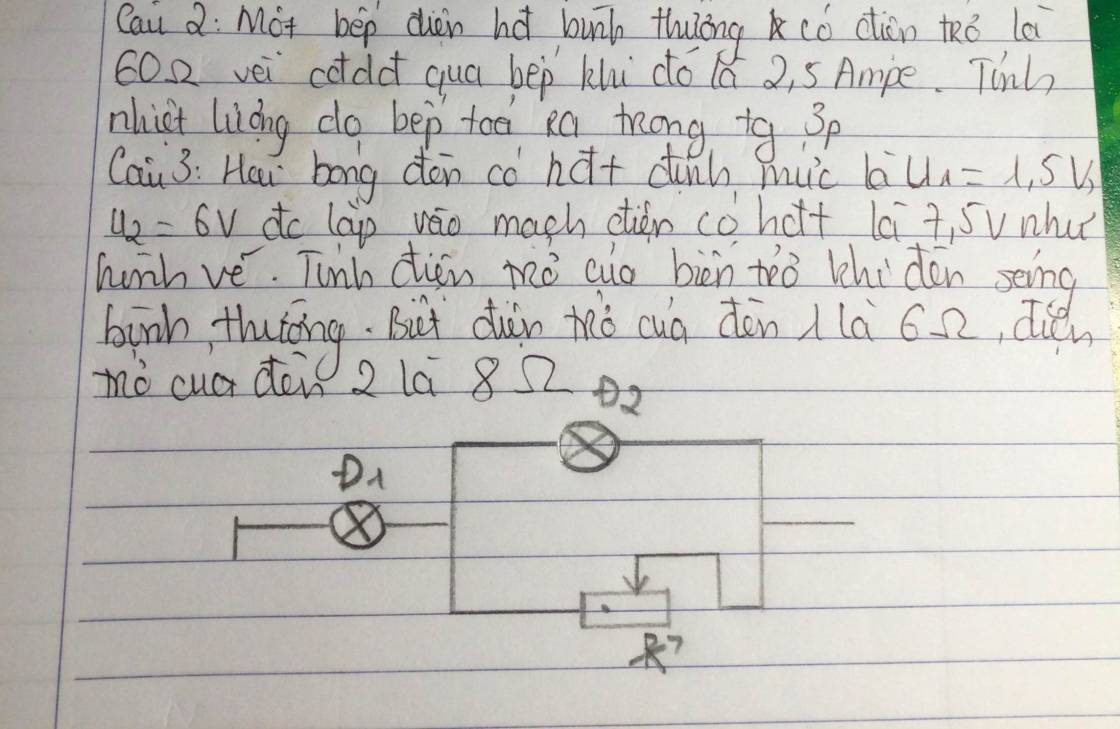
Mọi người ơi giúp em 2 câu này với ạ. Em đang cần gấp ạa🥲
Câu 2.
Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:
\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)
Câu 3.
\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)
\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)
\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)
\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)
Đúng 1
Bình luận (0)
Giúp e với ạa. E đang cần gấpp🥲

 Giúp em hết luôn được không ạa em đang gấp lắmm ạa:((, EM CẢM ƠN NHIỀUUU ẠA
Giúp em hết luôn được không ạa em đang gấp lắmm ạa:((, EM CẢM ƠN NHIỀUUU ẠA
1 Kai is tired because he stayed up late watching TV
2 Since I have a broken leg, I fell over while I was playing basketball
3 Sehun is going to be late for school as the bus is late
4 Because Lisa was careless, she broke the cup
5 Rose wants to go home since she feels sick
Đúng 0
Bình luận (0)
6 Jimin is hungry as he hasn't eaten all day
7 Since plastic bags are very hard to dissolve, they will cause pollution
8 People reuse and recycle bottles and cans as they want to reduce garbage
9 The sea is becoming increasingly polluted since people drop garbage into the sea
10 We shouldn't throw trash onto the water as polluted water can directly do harm to people's health and kill fish
Đúng 0
Bình luận (0)
11 Because of her illness, Lisa didn't go to work yesterday
12 Because of missing the first bus, he came to the office 10 minutes late
13 Because of the bad weather, they canceled the trip to the countryside
14 Because of her richness, she lives happily
15 Because of the heavy rain, we didn't go out
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
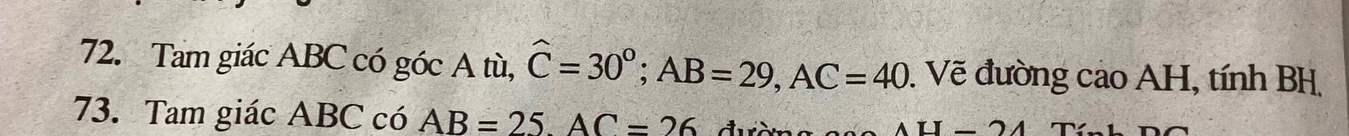 bài 72 giúp em 🥲🥲
bài 72 giúp em 🥲🥲
\(72.\)
Xét tam giác AHC vuông tại H ta có:
\(\sin C=\dfrac{AH}{AC}\) (Tỉ số lượng giác).
\(\Rightarrow\sin30^o=\dfrac{AH}{40}.\Rightarrow AH=20.\)
Xét tam giác AHB vuông tại H:
\(AB^2=AH^2+BH^2\left(Pytago\right).\)
\(\Rightarrow29^2=20^2+BH^2.\\ \Leftrightarrow BH^2=29^2-20^2.\\ \Rightarrow BH=21.\)
Đúng 4
Bình luận (1)
Xét tam giác vuông AHC có:
Góc HCA = 30 độ => Tam giác AHC là tam giác nửa đều
=> AH=\(\dfrac{1}{2}\) AC ( Tính chất tam giác nửa đều )
=> AH = 20
Xét tam giác AHB có:
AH2+HB2 =AB2( Định lý Py ta go )
=> BH= 21
Vậy BH=21
còn hình bn tự vẽ nhé
Đúng 2
Bình luận (1)
anh cj giúp em vs em cần gấp ạ 🥲🥲
Gọi vận tốc xe 1 và xe 2 lần lượt là a,b
Theo đề, ta có:
1/4a=1/3b và 1,6(a+b)=112
=>a=40; b=30
Đúng 0
Bình luận (0)
Giúp em với mn ơi🥲🥲 câu 1,3,4,6 ạ
Giúp em vs ạa, gấppp lắmmm, em cảm ơn ạa
Đọc tiếp
Giúp em vs ạa, gấppp lắmmm, em cảm ơn ạa



Bạn chia nhỏ nội dung ra để dc trợ giúp nhé
Đúng 0
Bình luận (0)
SOS. Giúp em với. Cần gấp 🙏🙏🙏🥲🥲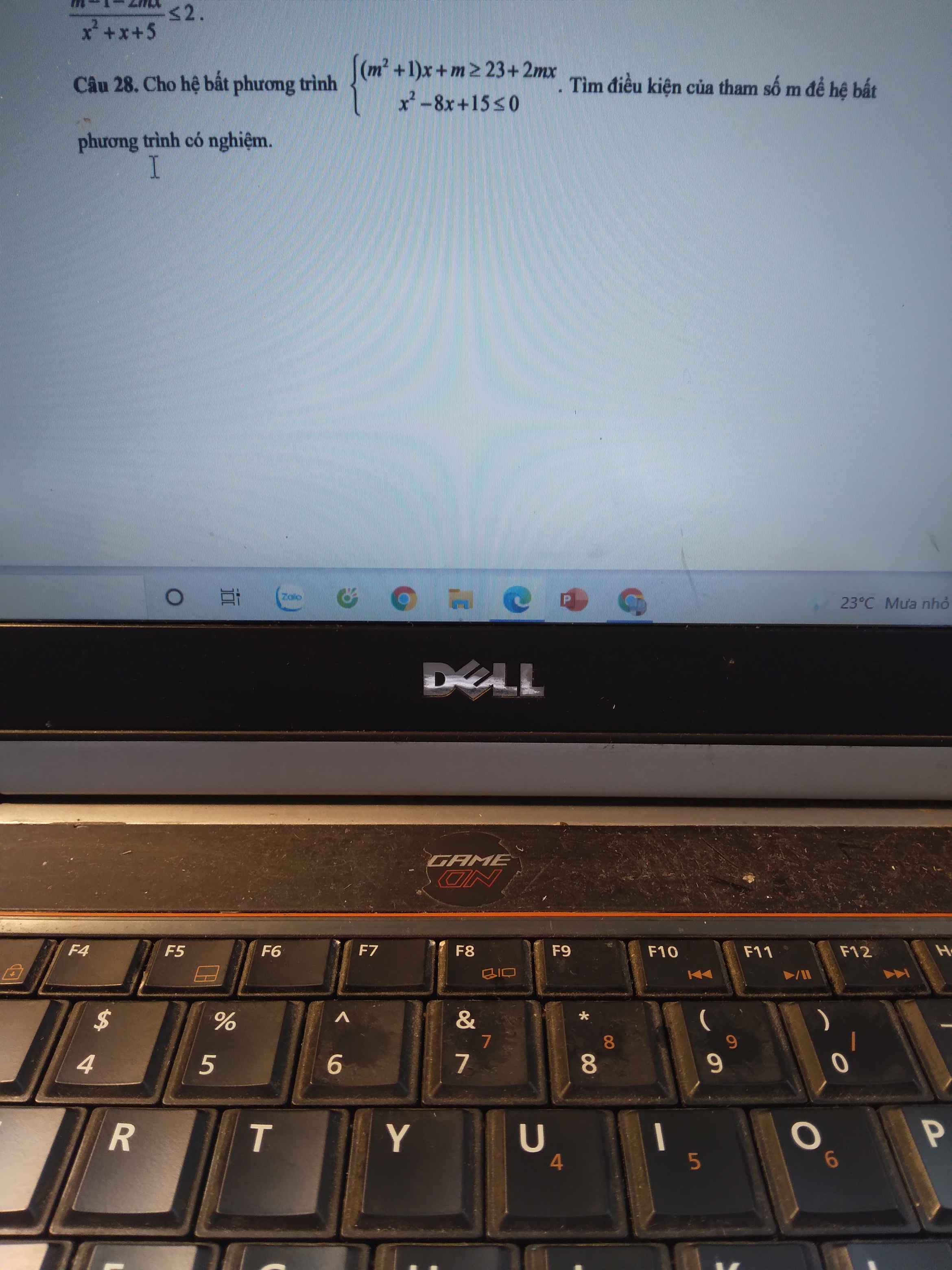
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)
Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)
\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)
\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)
- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)
- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)
\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)
Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)
\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)
\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
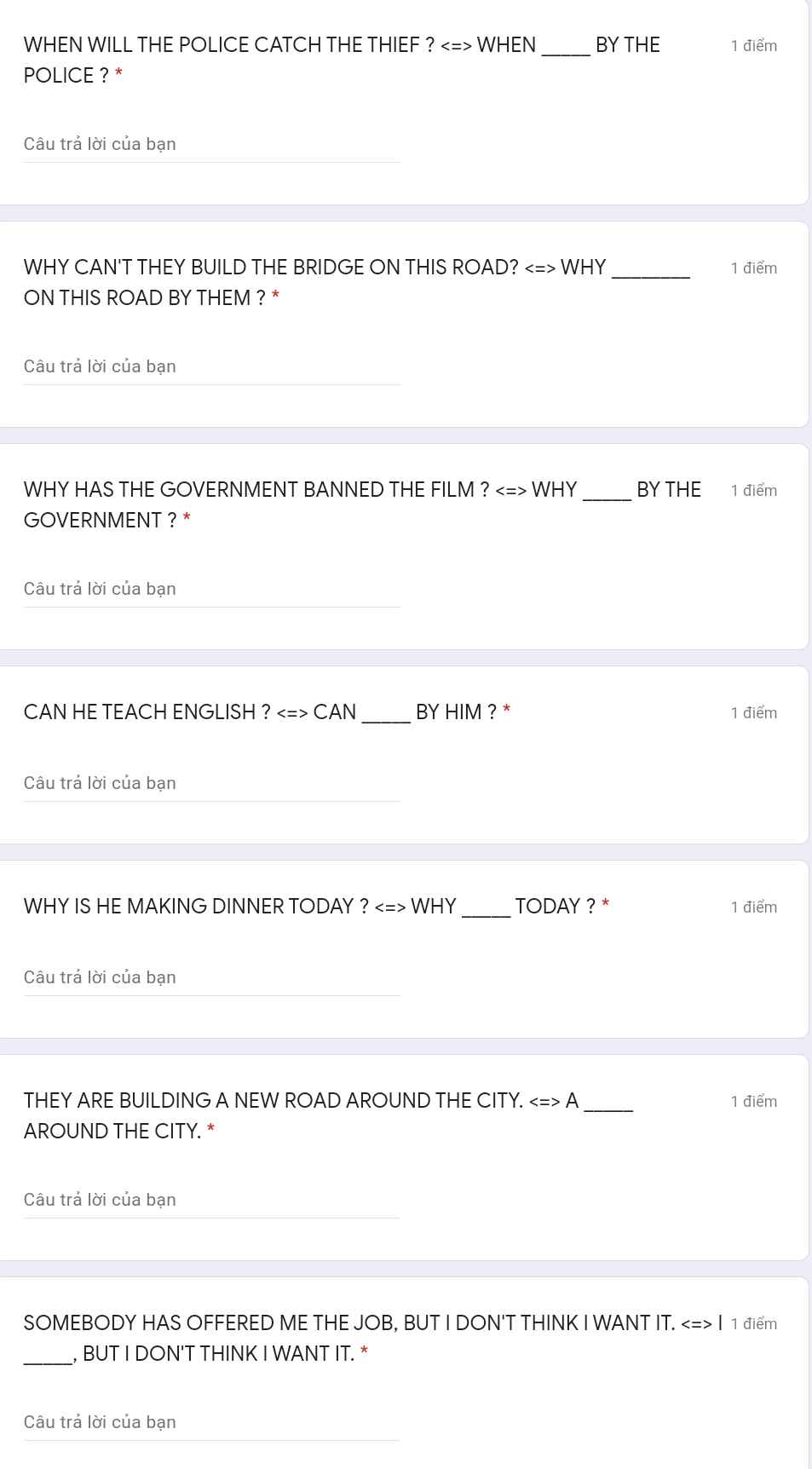 giúp em với ạa, bài này là bài tập không phải thi đâu ạa
giúp em với ạa, bài này là bài tập không phải thi đâu ạa


















