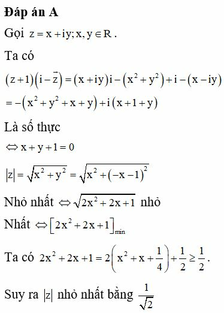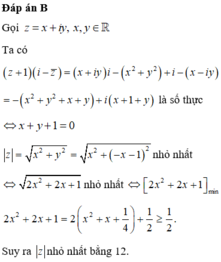số giá trị của x thỏa mãn 2015Ix-1I+(x-1)=2016Ix-1I

Những câu hỏi liên quan
Số giá trị của x thỏa mãn: (x2 + 1) + Ix - 1I + Ix3 + 1I = 0 là:
giá trị của x <0 thỏa mãn :Ix^2+1I=5
tao giai luon
Ix^2I=5-1
Ix^2I=4
=>X.2=4
x=4/2
x=2
nếu x<0 thì x=-2
Đúng 0
Bình luận (0)
tìm giá trị x thỏa mãn I2x+3I + I2x-1I = 8/3(x+1)^2+2
Tập hợp các giá trị của x thỏa mãn Ix + 1I + I1 - xI = 2 là {........}
x = {3, 4 , 4,6,7,8,9,10,.....}
li-ke mình nhé
Đúng 0
Bình luận (0)
Số giá trị của x thỏa mãn:Ix2+1I=5 là......
Tìm số nguyên x thỏa mãn I2x+1I + I2x-1I = 12
| 2x + 1 | + | 2x - 1 |
=> | 2x + 1 | = 12
2x = 12 - 1
2x = 11
x = 11 : 2
x = 5,5
=> | 2x - 1 | = 12
2x = 12 + 1
2x = 13
x = 13 : 2
x = 6,5
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
+
1
i
-
z
¯
là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 1 i - z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
![]()
![]()
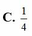
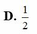
Cho số phức z thỏa mãn điều kiện
z
+
1
i
-
z
¯
là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 1 i - z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
![]()
![]()
![]()
![]()
Đáp án A
Gọi z = x + i y , x , y ∈ ℝ
z - 1 - i = 1 ⇔ x + i y - 1 - i = 1
⇔ x - 1 2 + y - 1 2 = 1 2 C
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S,
ta có O P ≤ O M + M P
do đó số phức tương ứng với P có môđun lớn nhất
khi và chỉ khi OP lớn nhất
OP = OM + MP
Tương đương 3 điểm O, M, P thẳng hàng
và M nằm giữa O và P
⇔ P ≡ P ' x P > 1
Phương trình đường thẳng OI: y = x
Tọa độ P’ là nghiệm của hệ phương trình :

Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
+
1
i
−
z
¯
là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng A.
1
4
B.
1
2
C.
1
2
D. 1
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 1 i − z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
A. 1 4
B. 1 2
C. 1 2
D. 1