Cho hình thang ABCD (AB//CD) có DAB = DBC. Tính độ dài cạnh BD biết AB=4 cm, DC=9 cm.

Những câu hỏi liên quan
Cho hình thang ABCD (AB//CD) và AB<CD Biết góc DAB = góc DBC; DC= 27cm, AB=12cm.
a)CM: tam giác ABD ~ tam giác DBC
b)Tính độ dài đoạn thẳng BD
c)Phân giác góc DBC cắt DC tại I. Tính DI biết AD = 14 cm.
T cần câu c thôi giúp t điiiii
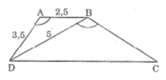
Cho hình thang ABCD (AB//CD và góc DAB=góc DBC)biết AB=2,5 cm ; AD=3,5 cm ; BD=5cm
a) Chứng minh ; tam giác ABD đồng dạng với tam giác BDC.
b) Tính độ dài các cạnh BC và CD.
c) Chứng minh :\(\frac{SABC}{SBDC}=\frac{1}{4}\)
a: Xét ΔABD và ΔBDC có
\(\widehat{ABD}=\widehat{BDC}\)
\(\widehat{A}=\widehat{DBC}\)
Do đó: ΔABD\(\sim\)ΔBDC
b: Ta có: ΔABD\(\sim\)ΔBDC
nên \(\dfrac{AB}{BD}=\dfrac{BD}{DC}=\dfrac{AD}{BC}\)
\(\Leftrightarrow\dfrac{5}{DC}=\dfrac{1}{2}=\dfrac{3.5}{BC}\)
=>DC=10; BC=7
c: Ta có: ΔABD\(\sim\)ΔBDC
nên \(\dfrac{S_{ABD}}{S_{BDC}}=\left(\dfrac{AB}{BD}\right)^2=\dfrac{1}{4}\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( AB // CD) . Biết AB = 3 cm; AD = 4 cm ; BD = 6cm và góc DAB= góc DBC
a.Chứng minh tam giác ADB đồng dạng tam giác BCD
b.Tính độ dài BC và CD.
c.Tính tỉ số diện tích của hai tam giác ADB và BCD.
a. vì AB//CD => góc ABD=góc BDC
xét tam giác ADB và tam giác BCD có:
góc DAB=góc DBC (gt)
góc ABD= góc BDC (cmt)
=> tam giác ADB ~ tam giác BCD (c.c)
b. vì tam giác ADB ~ tam giác BCD
=> \(\dfrac{AD}{BC}\)=\(\dfrac{AB}{BD}\)=\(\dfrac{DB}{CD}\)
=> BC= \(\dfrac{AD.BD}{AB}\)= \(\dfrac{4.6}{3}\)= 8(cm)
=> CD= \(\dfrac{BD^2}{AB}\)= \(\dfrac{6^2}{3}\)= 12 (cm)
Đúng 1
Bình luận (0)
Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠ (DAB) = ∠ (DBC). Tính độ dài BC, CD.
Vì
△
ABD ∼
△
BDC nên: 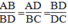
Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có:
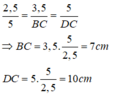
Đúng 0
Bình luận (0)
Cho hình bên, ABCD là hình thang ( AB//CD ) có AB 12,5cm; CD 28,5cm;
D
A
B
^
D
B
C
^
. Tính độ dài đoạn BD gần nhất bằng bao nhiêu? A. 17,5 B. 18 C. 18,5 D. 19
Đọc tiếp
Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; D A B ^ = D B C ^ . Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5
B. 18
C. 18,5
D. 19
Xét Δ ABD và Δ BDC có:
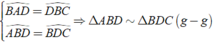
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x 2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.
Đúng 0
Bình luận (0)
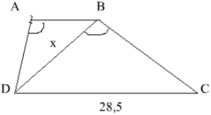
Cho hình thang ABCD (AB//CD) với AB 12,5cm; CD 28,5cm;góc DAB bằng góc DBC. Tính độ dài đoạn thẳng BD.
Đọc tiếp
Cho hình thang ABCD (AB//CD) với AB= 12,5cm; CD = 28,5cm;góc DAB bằng góc DBC. Tính độ dài đoạn thẳng BD.
Cho hình thang ABCD (AB//CD) có góc DAB= góc DBC và : AD= 3cm , AB= 5cm , BC= 4cm.
a, Chứng minh tam giác DAB đồng dạng với tam giác CBD
b, tính độ dài của DB, DC
c, Tính diện tích hình thang ABCD biết diện tích tam giác ABD = 5 cm vuông .
Mọi người giúp mình với xin chân thành cảm ơn nhiều !
Cho hình thang ABCD [ AB //CD ] .Biết AB = 2,5cm ; AD = 3,5cm ; BD = 5 cm ; và góc DAB = DBC .
a] Chứng minh hai tam giác ADB và BCD đồng dạng .
b] Tính độ dài các cạnh BC và CD .
c] Tính tỉ số diện tích hai tam giác ADB và BCD
a) Xét 2 tam giác ADB và BCD có:
góc DAB = góc DBC (gt)
góc ABD = góc BDC ( so le trong )
nên tam giác ADB đồng dạng với tam giác BDC.(1)
b) Từ (1) ta có AB/BC = DB/CD = AB/BD
hay AD/BC = AB/BD ⇔ 3,5/BC = 2,5/5
➩ BC= 3,5 . 5/2,5 = 7 (cm)
ta lại có: DB/CD = AB/BD ⇔ 5/CD = 2,5/5
==> CD = 5.5/2,5 =10 (cm)
c) Từ (1) ta được:
AD/BC = DB/CD = AB/BD
hay 3.5/7 = 5/10 = 2,5/5 = 1/2 .
ta nói tam giác ADB đồng dạng với tam giác BCD theo tỉ số đồng dạng là 1/2
mà tỉ số diện tích bằng bình phương tỉ số động dạng
do đó S ADB/ S BCD = (1/2)2 = 1/4
Gửi bạn nhé.Chữ xấu ráng chịu

a, Xét tam giác ADB và tam giác BCD ta có
^DAB = ^DBC ( gt )
^BDC = ^ABD ( so le trong )
Vậy tam giác ADB ~ tam giác BCD ( g.g )
Xem thêm câu trả lời
Cho hình thang ABCD (AB//CD) có AB =2,5cm;AD=3,5 cm;BD=5cm và\(\widehat{DAB}=\widehat{DBC}\)
a)CM:\(\Delta ADB\infty\Delta BCD\)
b)tính độ dài CD
\(\infty\):dấu đồng dạng


















