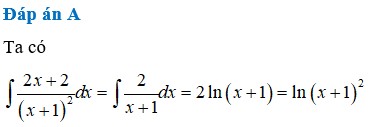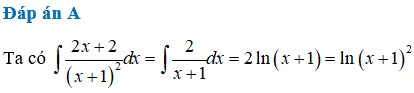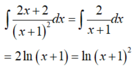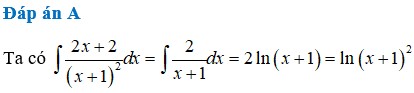Tìm nguyên hàm của y=x+1/x²+2x+2

Những câu hỏi liên quan
Tìm nguyên hàm của hàm số \(f\left(x\right)=\dfrac{x^2+2x}{x+1}\).
Lời giải:
\(\int f(x)dx=\int \frac{x^2+2x}{x+1}dx=\int \frac{(x+1)^2-1}{x+1}dx=\int (x+1-\frac{1}{x+1})dx\)
\(=\int (x+1)dx-\int \frac{1}{x+1}dx=\frac{x^2}{2}+x-\ln |x+1|+c\)
Đúng 3
Bình luận (0)
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là A.
ln
(
x
+
1
)
2
B.
ln...
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
A. ln ( x + 1 ) 2
B. ln 2 ( x + 1 )
C. ln ( x 2 + 2 x )
D. ln 2 ( x 2 + 2 x )
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là A.
ln
(
x
+
1
)
2
B.
ln...
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
A. ln ( x + 1 ) 2
B. ln 2 ( x + 1 )
C. ln ( x 2 + 2 x )
D. ln 2 ( x 2 + 2 x )
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
![]()
![]()
![]()
![]()
Một nguyên hàm của hàm số
y
2
x
+
2
(
x
+
1
)
2
là A.
ln
(
x
+
1
)
2
B.
ln...
Đọc tiếp
Một nguyên hàm của hàm số y = 2 x + 2 ( x + 1 ) 2 là
A. ln ( x + 1 ) 2
B. ln 2 ( x + 1 )
C. ln ( x 2 + 2 x )
D. ln 2 ( x 2 + 2 x )
a)Cho hàm số \(y=\frac{5}{2x+3}\)
Tìm giá trị của x để hàm số nhận giá trị nguyên.
b)Cho hàm số \(y=\frac{-5}{2x-1}\)
Tìm giá trị của x để hàm số nhận giá trị nguyên.
Tìm nguyên hàm của các hàm số sau:
a) \(\int\left(6x-\dfrac{1}{sin^2x}+1\right)dx\)
b) \(\int\dfrac{x^3+2x^2-1}{x^2}dx\)
Tìm nguyên hàm của hàm số:
1. \(f\left(x\right)=\left(2x-1\right)e^{\dfrac{1}{x}}\)
2. \(f\left(x\right)=e^{3x}.3^x\)
2.
\(I=\int e^{3x}.3^xdx\)
Đặt \(\left\{{}\begin{matrix}u=3^x\\dv=e^{3x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=3^xln3dx\\v=\dfrac{1}{3}e^{3x}\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}\int e^{3x}.3^xdx=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}.I\)
\(\Rightarrow\left(1+\dfrac{ln3}{3}\right)I=\dfrac{1}{3}e^{3x}.3^x\)
\(\Rightarrow I=\dfrac{1}{3+ln3}.e^{3x}.3^x+C\)
Đúng 1
Bình luận (0)
1.
\(I=\int\left(2x-1\right)e^{\dfrac{1}{x}}dx=\int2x.e^{\dfrac{1}{x}}dx-\int e^{\dfrac{1}{x}}dx\)
Xét \(J=\int2x.e^{\dfrac{1}{x}}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{\dfrac{1}{x}}\\dv=2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\dfrac{e^{\dfrac{1}{x}}}{x^2}dx\\v=x^2\end{matrix}\right.\)
\(\Rightarrow J=x^2.e^{\dfrac{1}{x}}+\int e^{\dfrac{1}{x}}dx\)
\(\Rightarrow I=x^2.e^{\dfrac{1}{x}}+C\)
Đúng 1
Bình luận (1)
Để tìm nguyên hàm của hàm số, ta cần xác định giá trị của hàm tại một điểm nào đó.
Trong trường hợp này, ta chọn điểm nhân nguyên tố nhất là 3.
Để tính giá trị của hàm tại điểm 3, ta đặt x=3 vào hàm số:
f ( x )
( 2 x − 1 ) e 1 x
= ( 2 ( 3 ) − 1 ) e 1 ( 3 )
= ( 6 − 1 ) e 1 3
= ( 5 ) e 1 3
f ( x )
e 3 x
= e 3 ( 3 )
= e 3 3
Ta tiến hành tính toán:
f ( 3 )
( 5 ) e 1 3
= 5 e 1 3
f ( 3 )
e 3 3
= e 3 3
Như vậy, giá trị của hàm tại điểm 3 là 5e^3 hoặc e^33, tùy thuộc vào hàm số cụ thể.
Tóm lại, để tìm nguyên hàm của hàm số, ta đã tìm được rằng giá trị của hàm tại điểm 3 là 5e^3 hoặc e^33, tùy thuộc vào hàm số cụ thể.
Đúng 0
Bình luận (1)
Bài 1. Cho hàm số y 2x-1a) Tính giá trị của hàm số y khi x0; x1; x -2b) Tìm giá trị của x khi y3Bài 2. Cho hàm số y -3xa) Vẽ đồ thị hàm sốb) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Đọc tiếp
Bài 1. Cho hàm số
y= 2x-1
a) Tính giá trị của hàm số y khi x=0; x=1; x= -2
b) Tìm giá trị của x khi y=3
Bài 2. Cho hàm số
y= -3x
a) Vẽ đồ thị hàm số
b) Tìm trên đồ thị hàm số điểm có hoành độ bằng 2
c) Tìm trên đồ thị hàm số điểm có tung độ bằng -6
Bài 1:
a: x=0 => y=-1
x=1 =>y=1
Đúng 1
Bình luận (0)