 mng giải giúp mik vs ạ
mng giải giúp mik vs ạ

Những câu hỏi liên quan
 mng giải giúp mik vs ạ
mng giải giúp mik vs ạ
 mng giải giúp mik vs ạ
mng giải giúp mik vs ạ
 mng giải giúp mik vs ạ
mng giải giúp mik vs ạ
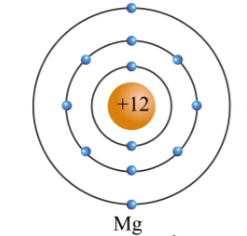
T có 3 lớp e, có 2e ở lớp ngoài cùng
Cấu hình của T : 1s22s22p63s2
T có số thứ tự 12 , chu kì 3, nhóm IIA
Đúng 1
Bình luận (0)
 mng giải giúp mik vs ạ
mng giải giúp mik vs ạ
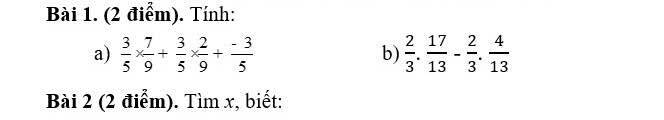 mng giải giúp mik vs ạ
mng giải giúp mik vs ạ
a) \(\dfrac{3}{5}\times\dfrac{7}{9}+\dfrac{3}{5}\times\dfrac{2}{9}+\dfrac{-3}{5}\)
\(=\dfrac{3}{5}\times\dfrac{7}{9}+\dfrac{3}{5}\times\dfrac{2}{9}+\dfrac{3}{5}\times\left(-1\right)\)
\(=\dfrac{3}{5}\times\left(\dfrac{7}{9}+\dfrac{2}{9}-1\right)\)
\(=\dfrac{3}{5}\times\left(1-1\right)\)
\(=\dfrac{3}{5}\times0=0\)
b) \(\dfrac{2}{3}\cdot\dfrac{17}{13}-\dfrac{2}{3}\cdot\dfrac{4}{13}\)
\(=\dfrac{2}{3}\cdot\left(\dfrac{17}{13}-\dfrac{4}{13}\right)\)
\(=\dfrac{2}{3}\cdot1=\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
giúp mình giải bài này vs ạ , mng ko chép mạng hộ mik nhé!. Thanks mng nhiều ạ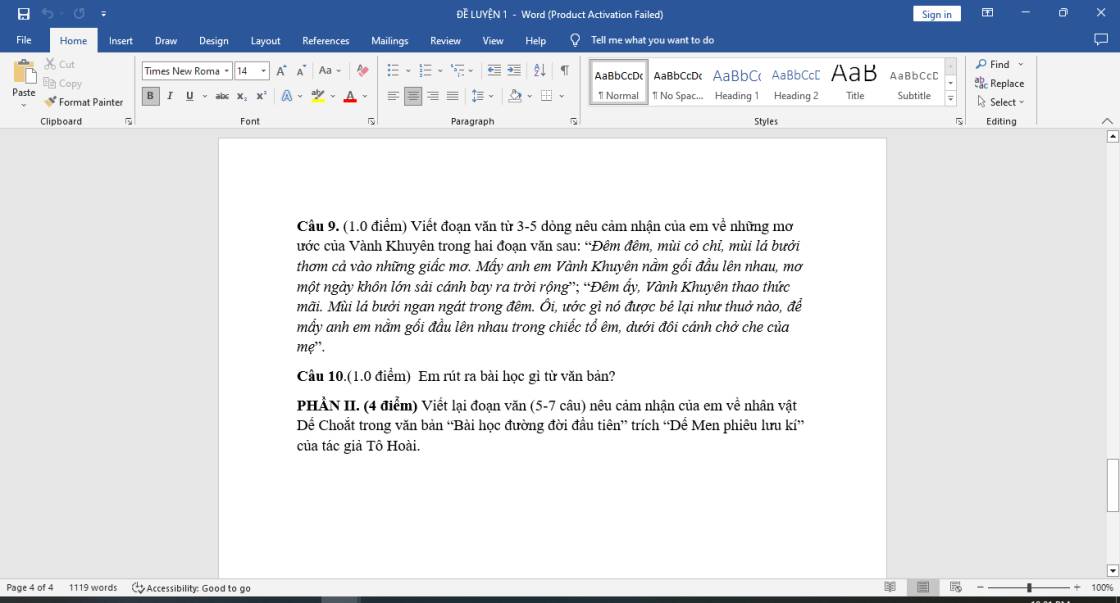
Bạn có thể đăng lại rồi chia nhỏ câu hỏi ra được không ạ? nếu có thể thì đăng full toàn bộ văn bản lên nữa để làm được câu 4
Đúng 0
Bình luận (0)
mng giải giúp mik vs ạ, vẽ hộ cả hình với
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
Đúng 1
Bình luận (0)
Giải giúp mik câu 1 và c3 vs ạ . Cảm ơn mng
3:
#include <bits/stdc++.h>
using namespace std;
double x,y;
int main()
{
cin>>x>>y;
cout<<fixed<<setprecision(2)<<sqrt(x*x+y*y);
return 0;
}
Đúng 0
Bình luận (1)
Giúp mik vs ạ, mik đang cần gấp. Mong mng giúp ạ

e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)
Đúng 0
Bình luận (1)
\(A=\dfrac{-4x^2+x^2-2x+1-x^2-2x-1}{\left(1-x\right)\left(1+x\right)}=\dfrac{-4x\left(x+1\right)}{\left(1-x\right)\left(1+x\right)}=\dfrac{4x}{x-1}\\ C=\dfrac{-x^2-4x-4+x^2-4x+4-4x^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{-4x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x}{2-x}\\ E=\dfrac{x^2-9-x^2+4x-4-x^2+9}{\left(x-2\right)\left(x+3\right)}=\dfrac{-\left(x-2\right)^2}{\left(x-2\right)\left(x+3\right)}=\dfrac{2-x}{x+3}\)
Đúng 0
Bình luận (0)











