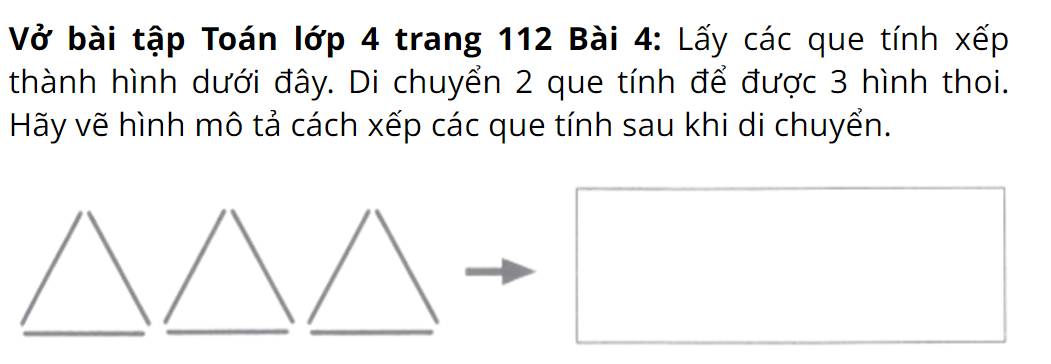
 Giúp em bài này với ạ, em cảm ơn!
Giúp em bài này với ạ, em cảm ơn!
Giúp em bài này với ạ. Em cám ơn ạ 🤭
Hello! John.
OK. So we'll go on a sightseeing tour by bikes at weekend
Giúp em bài này với ạ. Em cám ơn ạ 😆
Câu 4:
4.1/ Ta có: \(n_{NaCl}=2,5.0,4=1\left(mol\right)\)
\(\Rightarrow m_{NaCl}=1.58,5=58,5\left(g\right)\)
4.2/ Ta có: \(n_{Zn}=\dfrac{13}{65}=0,2\left(mol\right)\)
a, PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
_____0,2___________0,2____0,2 (mol)
b, \(V_{H_2}=0,2.22,4=4,48\left(l\right)\)
c, \(m_{ZnCl_2}=0,2.136=27,2\left(g\right)\)
Bạn tham khảo nhé!
giúp em bài này với ạ. em cám ơn
\(\dfrac{2020}{2019}>\dfrac{2019}{2020}\Rightarrow0< a< 1\)
\(log_ba< 1\Rightarrow b>1\)
\(P=log_b^2a+log_b^22-\dfrac{m^2log_2b}{log_2a}+2\left(log_ba-2log_b2\right)-\dfrac{4^{ab^2}-2m.2^{ab^2}}{log_ba}\)
\(=log_b^2a+log_b^22+2log_ba-4log_b2-\dfrac{4^{ab^2}-2m.2^{ab^2}+m^2}{log_ba}\)
\(=\left(log_ba+1\right)^2+\left(log_b2-2\right)^2+\dfrac{\left(2^{ab^2}-m\right)^2}{-log_ba}-5\ge-5\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}log_ba=-1\\log_b2=2\\2^{ab^2}=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{2}}\\b=\sqrt{2}\\m=2^{ab^2}=2^{\sqrt{2}}\end{matrix}\right.\)
Sau khi tính lại thì không có đáp án nào đúng :(
Giúp em 2 bài này với ạ, em cám ơn.
Câu 96: D. AB > CD (do AB là đường kính; CD là dây).
Câu 97: A. IC = ID (do CD \(\perp\) AB; CD là dây; AB là đường kính).
Mn giải giúp em bài này với ạ. Em cám ơn nhiều ah
Giúp em bài này với ạ.Em cám ơn ạ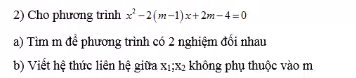
\(\Delta'=\left(m-1\right)^2-\left(2m-4\right)=\left(m-2\right)^2+1>0;\forall m\)
\(\Rightarrow\) Pt đã cho luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=2m-4\end{matrix}\right.\) (1)
a. Pt có 2 nghiệm đối nhau khi:
\(x_1+x_2=0\Leftrightarrow2m-2=0\Rightarrow m=1\)
b. Trừ vế cho vế của (1) ta được:
\(x_1+x_2-x_1x_2=2m-2-\left(2m-4\right)\)
\(\Leftrightarrow x_1+x_2-x_1x_2=2\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
Giúp em bài này cần gấp chiều nay em nộp bài rồi ạ, em cám ơn nhiều
Gọi Kim loại Đó là A
\(A+2HCl\rightarrow ACl_2+H_2\)
tl1.......2.............1...........1(mol)
br 0,15....0,3.....0,15.....0,15(mol)
\(n_{H_2}=\dfrac{V}{22,4}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
\(M_A=\dfrac{m}{n}=\dfrac{3,6}{0,15}=24\left(\dfrac{g}{mol}\right)\)
Vậy A là Magie(Mg)
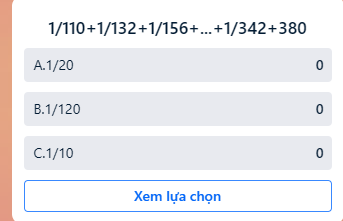
chỉ em bài này với em cám ơn ạ !
Lời giải:
\(\frac{1}{110}+\frac{1}{132}+\frac{1}{156}+...+\frac{1}{342}+\frac{1}{380}=\frac{1}{10\times 11}+\frac{1}{11\times 12}+...+\frac{1}{19\times 20}\)
\(=\frac{11-10}{10\times 11}+\frac{12-11}{11\times 12}+...+\frac{20-19}{19\times 20}=\frac{1}{10}-\frac{1}{11}+\frac{1}{11}-\frac{1}{12}+...+\frac{1}{19}-\frac{1}{20}\)
\(=\frac{1}{10}-\frac{1}{20}=\frac{10}{200}=\frac{1}{20}\)
Đáp án A.
Tinh nhanh :1313/2121x165165/143143x424242/151515
Các anh chị giúp em bài này với khó quá ....em cám ơn ạ !
1313/2121 x 165165/143143 x 424242/151515
=13/21 x 165/143 x42/15
=2
Rút gọn là sẽ xong, ko khó đâu
\(\frac{1313}{2121}\times\frac{165165}{143143}\times\frac{424242}{151515}=\frac{13}{21}\times\frac{165}{143}\times\frac{42}{15}=\frac{13\times165\times42}{21\times143\times15}\)
\(=\frac{13\times15\times11\times21\times2}{21\times13\times11\times15}=2\)
rút gọn
=13x165x42/21x143x15
=1x11x2/1x11x1
=2
giúp em câu này với ạ em cám ơn 