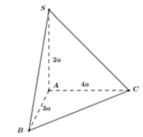
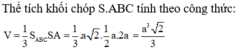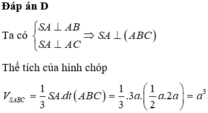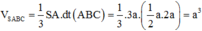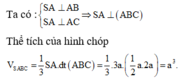cho một hình chóp S.ABC có SA vuông góc (abc) SA=AC=2a, AB=a, gócBAC=60°. Tính thể tích khối chóp

Những câu hỏi liên quan
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SAa, ABa, AC2a.
B
A
C
^
60
∘
. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC. A.
V
20
5
π
a
3...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=a, AB=a, AC=2a. B A C ^ = 60 ∘ . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC.
A. V = 20 5 π a 3 3
B. V = 5 6 π a 3
C. 5 5 π 2 a 3
D. V = 5 5 6 π a 3
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC),
S
A
a
,
A
B
a
,
A
C
2
a
,
B
A
C
60
°
. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC A.
V
20
5
π
a...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), S A = a , A B = a , A C = 2 a , B A C = 60 ° . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
A. V = 20 5 π a 3 3
B. V = 5 5 6 π a 3
C. V = 5 5 π 2 a 3
D. V = 5 6 π a 3
Đáp án B
Phương pháp:
- Chứng minh Δ A B C vuông tại B, tìm tâm và bán kính đường tròn ngoại tiếp tam giác đáy.
- Sử dụng công thức R 2 = h 2 4 + r 2 với R là bán kính hình cầu ngoại tiếp khối chóp, h là chiều cao, r là bán kính đường tròn ngoại tiếp đa giác đáy.
Cách giải:
Ta có: cos 60 ° = 1 2 = a 2 a → cos B A C = A B A C
⇒ Δ A B C vuông tại B.
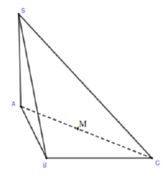
Gọi M là trung điểm AC.
⇒ M là tâm đường tròn ngoại tiếp Δ A B C
⇒ M A = M A = A C 2 = a

Gọi r là bán kính đường tròn ngoại tiếp tam giác đáy.
R là bán kính mặt cầu ngoại tiếp hình chóp.
h là chiều cao hình chóp.
Ta có công thức sau:
R 2 = h 2 4 + r 2 ⇒ R 2 = a 2 4 + a 2 = a 5 2
⇒ V = 4 3 π R 3 = 5 a 5 6
Chú ý khi giải:
HS cần linh hoạt trong việc chứng minh Δ A B C vuông tại B và biết sử dụng công thức liên hệ giữa R, r, h.
Đúng 0
Bình luận (0)
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB α . Áp dụng: Tính VS ABCD . trong trường hợp α 60 độ. Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC 120độ . Cho SA vuông góc với đáy và SC 2a .Tính thể tích hình chóp S.ABCD.Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC20 cm BC...
Đọc tiếp
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
Cho khối chóp S.ABC có SA vuông góc với đáy
A
B
C
,
S
A
a
2
.
. Đáy ABC vuông tại
A
,
A
B
a
,
A
C
2
a
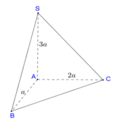
(tham khảo hình vẽ bên). Tính thể tích khối chóp S.ABC A.
a
3...
Đọc tiếp
Cho khối chóp S.ABC có SA vuông góc với đáy A B C , S A = a 2 . . Đáy ABC vuông tại A , A B = a , A C = 2 a (tham khảo hình vẽ bên). Tính thể tích khối chóp S.ABC
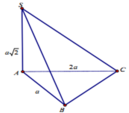
A. a 3 2 3
B. a 3 2
C. 2 a 3 2 3
D. a 3 2 6
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau,
AB
a
,
AC
2
a
,
SA
3
a
.
Tính thể tích của khối chóp S.ABC. A.
3
a
3
B.
2
a
3
C.
1
2
a
3...
Đọc tiếp
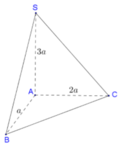
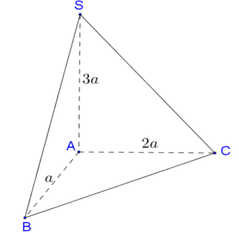
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, AB = a , AC = 2 a , SA = 3 a . Tính thể tích của khối chóp S.ABC.
A. 3 a 3
B. 2 a 3
C. 1 2 a 3
D. a 3
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, ABa. AC2a. SA3a. Tính thể tích của khối chóp S.ABC.
Đọc tiếp
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, AB=a. AC=2a. SA=3a. Tính thể tích của khối chóp S.ABC.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau,
A
B
a
,
A
C
2
a
,
S
A
3
a
. Tính thể tích của khối chóp S.ABC. A.
2
a
3
B.
2
a
3
C.
1
2
a
3...
Đọc tiếp
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, A B = a , A C = 2 a , S A = 3 a . Tính thể tích của khối chóp S.ABC.
A. 2 a 3
B. 2 a 3
C. 1 2 a 3
D. a 3
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SAa, ABa, AC2a, BAC
60
o
. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=a, AB=a, AC=2a, BAC= 60 o . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC
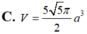
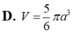
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Biết SA 2a và tam giác ABC vuông tại A có
AB
3
a
,
AC
4
a
.
Tính thể tích khối chóp S.ABC theo a A.
12
a
3
B.
6
a
3
C.
8
a
3
D. ...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Biết SA = 2a và tam giác ABC vuông tại A có AB = 3 a , AC = 4 a . Tính thể tích khối chóp S.ABC theo a
A. 12 a 3
B. 6 a 3
C. 8 a 3
D. 4 a 3