Nhờ thầy cô và các bạn hướng dẫn dùm em ạ
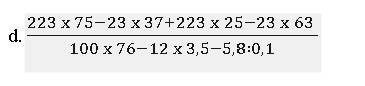
Nhờ các bạn và thầy cô hưỡng dẫn ạ...
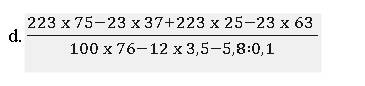
\(\dfrac{223\cdot75-23\cdot37+223\cdot25-23\cdot63}{100\cdot76-12\cdot3,5-5,8:0,1}\)
\(=\dfrac{223\left(75+25\right)-23\left(37+63\right)}{100\cdot76-42-58}\)
\(=\dfrac{100\cdot223-23\cdot100}{100\cdot76-100}\)
\(=\dfrac{100\left(223-23\right)}{100\left(76-1\right)}=\dfrac{200}{75}=\dfrac{8}{3}\)
Nhờ thầy cô hướng dẫn giải chi tiết bài này ạ.

Theo quan sát hình vẽ thì thực tế đã có 6 cái ghế
Vì mỗi ghế để 1 người ngồi nên 6 ghế có 6 người ngồi
tất cả có 19 người vậy số người chưa có ghế là :
19 - 6 = 13 (người )
vì mỗi người một ghế nên số ghế cần thêm là 16 ghế.
Sau đây là bài giải chi tiết em nhé :
Số ghế cần thêm là : 19 - 6 = 13 ( ghế )
Nhờ thầy cô hướng dẫn giải chi tiết bài 1.e) ở dưới ạ.

a, 41,51,61
b, 70, 90
c, 55, 66, 77
d, 15, 25
e, 34 (Từ số hạng thứ 3 = Tổng 2 số hạng trước nó:22=10+12; Số hạng thứ 4 = Số hạng thứ 2+ Số hạng thứ 3 = 12+22=34)
f, 30, 20
1,a,41,51,61 d,15,20,25
b,70,90 e, 34 (Từ số hạng thứ 3 = Tổng 2 số hạng trước nó:22=10+12; Số hạng thứ 4 = Số hạng thứ 2+ Số hạng thứ 3 = 12+22=34)
c,55,66,77 f,30,20
Nhờ thầy cô và các bạn giúp em ạ. Em cảm ơn.
14.
\(\left(ab+c\right)\left(bc+a\right)\le\dfrac{1}{4}\left(ab+bc+c+a\right)^2=\dfrac{1}{4}\left(a+c\right)^2\left(b+1\right)^2\)
Tương tự:
\(\left(ab+c\right)\left(ca+b\right)\le\dfrac{1}{4}\left(b+c\right)^2\left(a+1\right)^2\)
\(\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{4}\left(a+b\right)^2\left(c+1\right)^2\)
Nhân vế với vế và khai căn:
\(\left(ab+c\right)\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{8}\left(a+b\right)\left(b+c\right)\left(c+a\right)\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
Mặt khác ta có:
\(\left(a+1\right)\left(b+1\right)\left(c+1\right)\le\dfrac{1}{27}\left(a+b+c+3\right)^3=8\)
\(\Rightarrow\left(ab+c\right)\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{8}.8.\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Dấu "=" xảy ra khi...
15.
\(\Leftrightarrow\sum\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}\le2\)
\(\Leftrightarrow\sum\left(\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}-1\right)\le2-3\)
\(\Leftrightarrow\sum\dfrac{\left(b+c-a\right)^2}{2a^2+\left(b+c-a\right)^2}\ge1\)
Đặt \(\left\{{}\begin{matrix}b+c-a=x\\c+a-b=y\\a+b-c=z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{y+z}{2}\\b=\dfrac{x+z}{2}\\c=\dfrac{x+y}{2}\end{matrix}\right.\)
\(VT=\sum\dfrac{x^2}{2\left(\dfrac{y+z}{2}\right)^2+x^2}=\sum\dfrac{2x^2}{2x^2+\left(y+z\right)^2}\ge\sum\dfrac{2x^2}{2x^2+2\left(y^2+z^2\right)}=1\)
Dấu "=" xảy ra khi...
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Nhờ thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều ạ!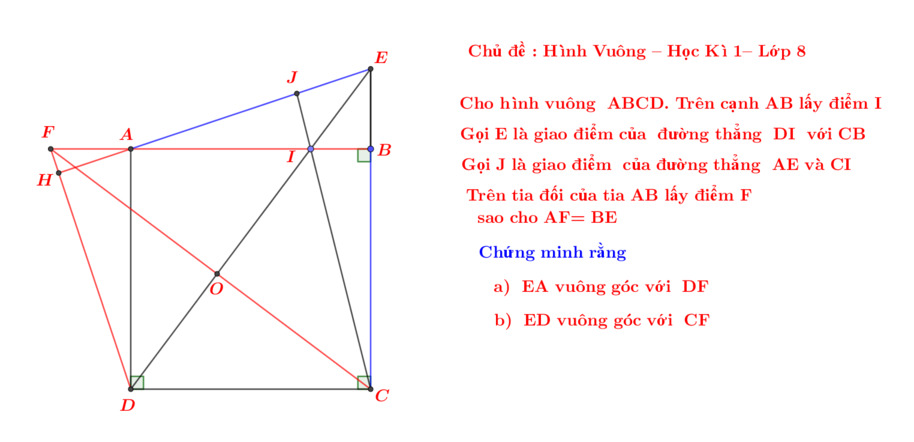
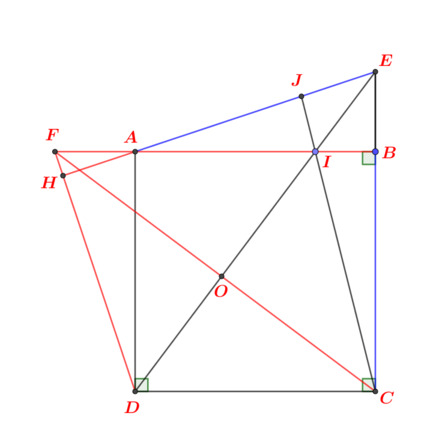
Nhờ thầy cô và các bạn giúp em câu 1.1.16 và 1.1.17 ạ. Em cảm ơn.
Nhờ thầy cô và các bạn trong nhóm giúp đỡ em với ạ!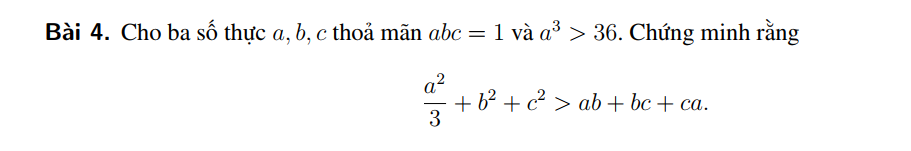
Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)