Phân tích đa thức thành nhân tử:
a) x^3+4x^2-7x-10
b) 8x^3(y+z)-y^3(z+2x)-z^3(2x-y)
Phân tích các đa thức sau thành nhân tử:
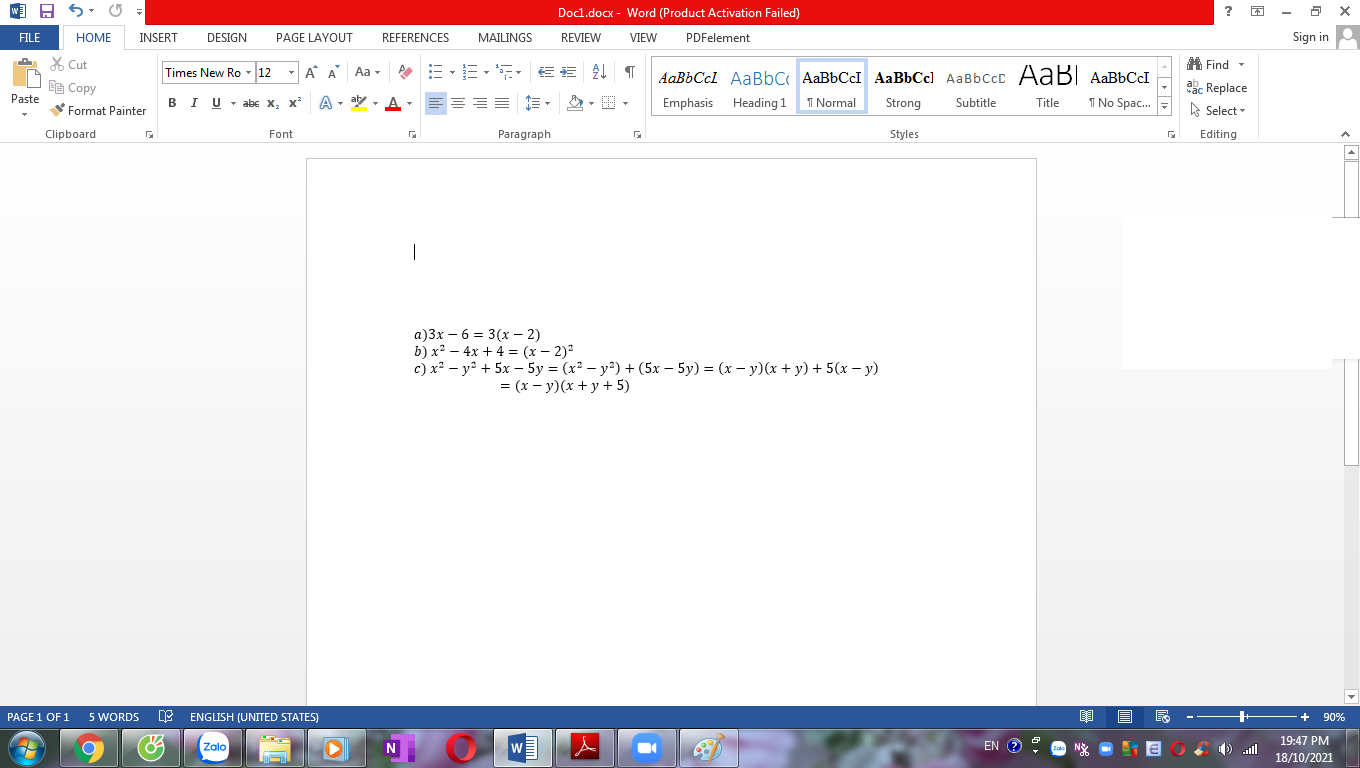
a) 3x-6
b) x2-4x+4
c) x2-y2+5x-5y
d) 8(x+y+z)3-(x+y)3-(y+z)3-(y+z)3-(z+x)3
Do câu d mình ko biết làm bởi v mình không làm được
Phân tích đa thức thành nhân tử:
a) x^3 - x^2 + 8x - 8
b) 8x^3 - 8x^2y + 2xy^2
c) (x^2 + y^2 - z^2)^2 - 4x^2y^2
d) (x^2 - y^2 - 5)^2 - 4(x^2y^2 + 4xy + 4)
e) x^3 - y^3 - 3x^2 + 3x - 1
a) (x3-x2)+(8x-8)=x(x-1)+8(x-1)=(x2+8)(x-1)
b) 8x3-8x2y+2xy2=2x(4x2-4xy+y2)
c) (x2+y2-z2)2 - 4x2y2=(x2+y2-z2)2 - (2xy)2=(x2+y2-z2-2xy)(x2+y2-z2+2xy)
Phân tích đa thức thành nhân tử:
a) 6x^2-12x-7x+14
b) 2x^2(y+2z)-2y^2(z+2x)-2z^2(x+2y)+9xyz
\(a,=6x\left(x-2\right)-7\left(x-2\right)=\left(6x-7\right)\left(x-2\right)\)
phân tích đa thức thành nhân tử: 8x3(y+z)-y3(z+2x)-z3(2x-y)
\(8x^3\left(y+z\right)-y^3\left(z+2x\right)-z^3\left(2x-y\right)\)
\(=8x^3\left(y+z\right)-y^3\left[\left(y+z\right)+\left(2x-y\right)\right]-z^3\left(2x-y\right)\)
\(=8x^3\left(y+z\right)-y^3\left(y+z\right)-y^3\left(2x-y\right)-z^3\left(2x-y\right)\)
\(=\left(y+z\right)\left(8x^3-y^3\right)-\left(2x-y\right)\left(y^3+z^3\right)\)
\(=\left(y+z\right)\left(2x-y\right)\left(4x^2+4xy+y^2\right)-\left(2x-y\right)\left(y+z\right)\left(y^2-xy+z^2\right)\)
\(=\left(y+z\right)\left(2x-y\right)\left(4x^2+4xy+y^2-y^2+xy-z^2\right)\)
\(=\left(y+z\right)\left(2x-y\right)\left(4x^2+5xy-z^2\right)\)
Phân tích đa thức thành nhân tử: 8x3(y+z)-y3(z+2x)-z3(2x-y)
Bây giờ mình đặt \(\left(2x;-y;z\right)=\left(a;b;c\right)\)với đa thức đã cho là S cho nó đẹp cái đã, cơ mà đề bài khúc cuối là cộng hay trừ thế
Nếu khúc cuối là trừ thì lúc này \(S=a^3\left(b+c\right)+b^3\left(c+a\right)-c^3\left(a+b\right)\)
Ta thấy biểu thức S gần đối xứng với các biến a,b,c
Với các biểu thức này thì thường dùng xét giá trị biến kiểu như thế này:
Nếu a=c thì thay vào S=b3(c+a)
Nếu b=c thì thay vào S=a3(b+c)
Do đó ta thấy S có dạng A.(b+c)(c+a), với a là một biểu thức bậc 2 với 3 biến a,b,c
Bây giờ mình đi tìm A như sau
Giả sử \(A=\alpha a^2+\beta b^2+\gamma c^2+uab+vbc+wca\)
Thử với các giá trị \(\cdot\left(a;b;c\right)=\left(1;2;3\right);\left(4;5;6\right);\left(7;8;9\right);...\)
Rồi tìm ra các hệ số của A rồi suy ra S bằng bao nhiêu đó
Phân tích các đa thức sau thành nhân tử:
a) x^3-4x^2+4x
b) x^2-2xy+y^2-9
c)2x^3-x^2-8x+4
d) x^2-y^2-5x+5y
e) 3x^2-6xy+3y^2-12z^2
f) x^3-4x^2+4x-xy^2
g) x^3-2x^2y+xy^2-25x
h) x^3-3x+2
i) 3x^2-7x-10
\(a,=x\left(x-2\right)^2\\ b,=\left(x-y\right)^2-9=\left(x-y-3\right)\left(x-y+3\right)\\ c,=x^2\left(2x-1\right)-4\left(2x-1\right)=\left(x-2\right)\left(x+2\right)\left(2x-1\right)\\ d,=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)=\left(x-y\right)\left(x+y-5\right)\\ e,=3\left[\left(x-y\right)^2-4z^2\right]=3\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x\left[\left(x-2\right)^2-y^2\right]=x\left(x-y-2\right)\left(x+y-2\right)\\ g,=x\left[\left(x-y\right)^2-25\right]=x\left(x-y-5\right)\left(x-y+5\right)\\ h,=x^3-x-2x+2=x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\\ =\left(x-1\right)\left(x^2+x-2\right)=\left(x-1\right)^2\left(x+2\right)\\ i,=3x^2+3x-10x-10=\left(x+1\right)\left(3x-10\right)\)
Phân tích đa thức thành nhân tử:
a) x^2y + 2xy^2 + xy
b) x^3 + x^2 – 4x – 4
c) x^2 – 2x – 15
d) x^2 – 4 + (x – 2)^2
e) x^2 – y^2 + 2x + 1
g) (x + 9)^2 – 36x^2
h) x^2 – 2xy + y^2 – z^2 + 2zt – t^2
i) x^3 – 3x^2 + 3x – 1 – y^3
\(a,=xy\left(x+2y+1\right)\\ b,=x^2\left(x+1\right)-4\left(x+1\right)=\left(x+1\right)\left(x-2\right)\left(x+2\right)\\ c,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ d,=\left(x-2\right)\left(x+2\right)+\left(x-2\right)^2=\left(x-2\right)\left(x+2+x-2\right)=2x\left(x-2\right)\\ e,=\left(x+1\right)^2-y^2=\left(x+y+1\right)\left(x-y+1\right)\\ g,=\left(x+9-6x\right)\left(x+9+6x\right)=\left(9-5x\right)\left(7x+9\right)\\ h,=\left(x-y\right)^2-\left(z-t\right)^2=\left(x-y-z+t\right)\left(x-y+z-t\right)\\ i,=\left(x-1\right)^3-y^3=\left(x-y-1\right)\left(x^2-2x+1+xy+y+y^2\right)\)
c: =(x-5)(x+3)
e: =(x+1-y)(x+1+y)
\(8x^3\left(y+z\right)-y^3\left(z+2x\right)-z^3\left(2x-y\right)\\ \).Phân tích đa thức trên thành nhân tử chung
=8x3y + z3y + 8x3z -2xz3 - y3(z +2x)= y(8x3+z3) +2xz(4x2-z2) - y3(2x+z) = y(2x+z)(4x2 - 2xz + z2) +2xz(2x+z)(2x-z) - y3(2x+z)
=(2x+z)(4x2y -2xyz + z2y + 4x2z -2xz2 - y3) = (2x+z)( 4x2y+ 4x2z - 2xyx- 2xz2 +z2y - y3) = (2x+z)[ 4x2(y+z) -2xz(y+z) + y(z+y)(z-y)]
= (2x+z)(y+z)( 4x2- 2xz +yz- y2) = (2x+z)(y+z)(4x2 - y2 -2xz + yz) = (2x+z)(y+z)[(2x-y)(2x+y) - z(2x-y)]
= (2x+y)(y+z)(2x-y)(2x+y-z)
Phân tích các đa thức sau thành nhân tử (bằng phương pháp đặt nhân tử chung)
a) 4x(2y - z) + 7y(z - 2y)
b) 2x(x + 3) + (3 + x)
c) 3x(2x - 1) + 7x2(1 = 2x)
d) y(x - z) + 7(z - x)
a) Ta có: \(4x\left(2y-z\right)+7y\left(z-2y\right)\)
\(=4x\left(2y-z\right)-7y\left(2y-z\right)\)
\(=\left(4x-7y\right)\left(2y-z\right)\)
b) Ta có: \(2x\left(x+3\right)+\left(3+x\right)\)
\(=\left(2x+1\right)\left(x+3\right)\)
c) Ta có: \(3x\left(2x-1\right)+7x^2\left(1-2x\right)\)
\(=3x\left(2x-1\right)-7x^2\left(2x-1\right)\)
\(=\left(3x-7x^2\right)\left(2x-1\right)\)