Cho tam giác ABC có AB=AC . gọi I là trung điểm của BC. a) chứng minh tam giác AIB = tam giác AIC. b) cm AI là tia pg của góc BAC. c) kẻ IH vuông góc AB tại H kẻ IK vuông góc với AC tại K . cm IA là tia pg của góc HIK.

Những câu hỏi liên quan
cho đoạn thẳng BC. gọi I là trung điểm của BC trên đường trung trực của đoạn thẳng BC láy điểm A (A khác I)
a) cm tam giác AIB=AIC
b)kẻ IH vuông góc AB, IK vuông góc AC, chứng minh IK vuông góc IK=IH
c) qua C kẻ Cx song song với AB cắt AI tại N . chứng minh CB là tia phân giác của góc ACN
Cho tam giác ABC, có AB = AC. Tia phân giác của góc A cắt BC tại I.
a) Chứng minh tam giác AIB = tam giác AIC
b) Từ I kẻ IH,IK lần lượt vuông góc với AB,AC (H thuộc AB, K thuộc AC). Chứng minh IH = IK
c) Gọi M là giao điểm của HI và AC, N là giao điểm của KI và AB, P là trung điểm của MN. Chứng minh A,I,P thẳng hàng
a: Xét ΔAIB và ΔAIC có
AB=AC
\(\widehat{BAI}=\widehat{CAI}\)
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>IB=IC và \(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAHI=ΔAKI
=>IH=IK
c: Xét ΔHIN vuông tại H và ΔKIM vuông tại K có
IH=IK
\(\widehat{HIN}=\widehat{KIM}\)
Do đó: ΔHIN=ΔKIM
=>IN=IM và HN=KM
ΔAHI=ΔAKI
=>AH=AK
AH+HN=AN
AK+KM=AM
mà AH=AK và HN=KM
nên AN=AM
=>A nằm trên đường trung trực của NM(1)
IN=IM(cmt)
nên I nằm trên đường trung trực của MN(2)
PN=PM
=>P nằm trên đường trung trực của MN(3)
Từ (1),(2),(3) suy ra A,I,P thẳng hàng
Đúng 2
Bình luận (1)
Cho đoạn thẳng BC, gọi I là trung điểm của BC. Trên đường trung trực của đoạn thẳng BC lấy điểm A ( A khác I)a) Chứng minh rằng tam giác AIB tam giác AIC (làm rồi)b) Kẻ IH vuông góc với AB, IK vuông góc với AC. Chứng minh rằng IHIK (làm rồi)c) Qua B kẻ Bx//AC cắt AI kéo dài tại E. Chứng minh BC là phân giác của góc ABEd) Chứng minh EA là tia phân giác của góc BACe) KI cắt BE tại M .Chứng minh góc BIM góc IACGiúp mình nha!
Đọc tiếp
Cho đoạn thẳng BC, gọi I là trung điểm của BC. Trên đường trung trực của đoạn thẳng BC lấy điểm A ( A khác I)
a) Chứng minh rằng tam giác AIB= tam giác AIC (làm rồi)
b) Kẻ IH vuông góc với AB, IK vuông góc với AC. Chứng minh rằng IH=IK (làm rồi)
c) Qua B kẻ Bx//AC cắt AI kéo dài tại E. Chứng minh BC là phân giác của góc ABE
d) Chứng minh EA là tia phân giác của góc BAC
e) KI cắt BE tại M .Chứng minh góc BIM = góc IAC
Giúp mình nha!
1: cho tam giác ABC có ABAC và M là trung điểm của AC và N là trung điểm của AB, BM và CN cắt nhau tại KChứng minh:a)tam giácBNCtam giác CMBb)tam giác BKC có KBKC2:Cho đoạn thẳng BC. Gọi I là trung điểm của BC trên đường trung trực của BC lấy điểm A (A khác I)1.CHỨNG MINH AIBAIC2.KẺ IH VUÔNG GÓC VỚI AB,KẺ IK VUÔNG GÓC VỚI ACA)chứng minh tam giác AHK CÓ HAI CẠNH BẰNG NHAUB)CM HK//BC
Đọc tiếp
1: cho tam giác ABC có AB=AC và M là trung điểm của AC và N là trung điểm của AB, BM và CN cắt nhau tại K
Chứng minh:a)tam giácBNC=tam giác CMB
b)tam giác BKC có KB=KC
2:Cho đoạn thẳng BC. Gọi I là trung điểm của BC trên đường trung trực của BC lấy điểm A (A khác I)
1.CHỨNG MINH AIB=AIC
2.KẺ IH VUÔNG GÓC VỚI AB,KẺ IK VUÔNG GÓC VỚI AC
A)chứng minh tam giác AHK CÓ HAI CẠNH BẰNG NHAU
B)CM HK//BC
Bài 4: Cho tam giác ABC cân tại A với AI là đường trung tuyến. a) Chứng minh tam giác AIB = tam giác AIC b) Kẻ IH vuông góc AB, IK vuông góc AC. Chứng minh: IH=IK.
a, Xét ΔAIB và ΔAIC có:
AB=AC (ΔABC cân tại A)
Chung AI
IB=IC (gt)
⇒ΔAIB = ΔAIC (c.c.c)
b, Xét ΔIHB và ΔIKC có:
\(\widehat{IHB}=\widehat{IHC}\left(=90^o\right)\)
IB=IC(gt)
\(\widehat{B}=\widehat{C}\) (ΔABC cân tại A))
\(\Rightarrow\)ΔIHB = ΔIKC (ch-gn)
\(\Rightarrow IH=IK\)(2 cạnh tương ứng)
Đúng 2
Bình luận (1)
Cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID = IA
a) Chứng minh tam giác ABI = tam giác ACI
b) Chứng minh AC // BD
c) Kẻ IK vuông góc với AB (K ϵ AB), IH vuông góc với CD (H ϵ CD). Chứng minh IK= IH
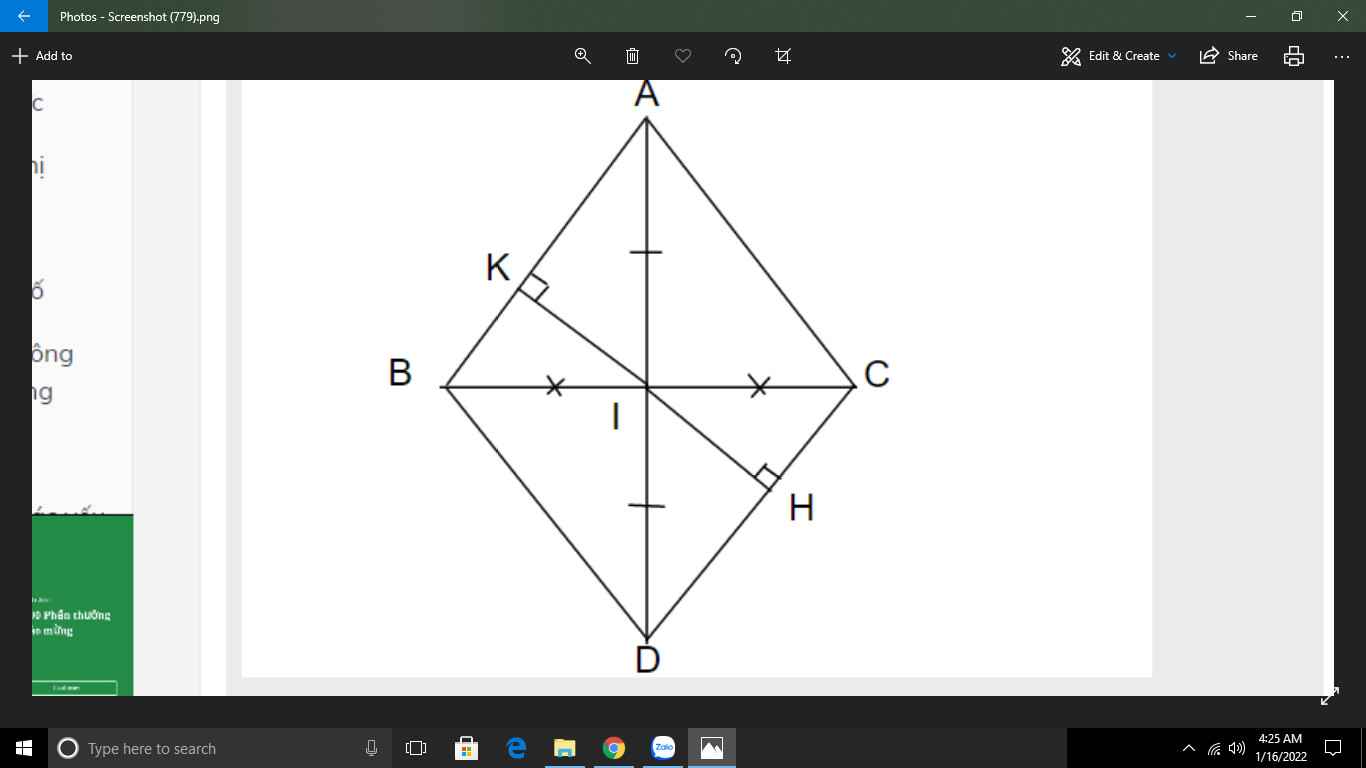
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)
Đúng 2
Bình luận (0)
Bài 1. Cho tam giác ABC cân tại A. Gọi I là trung điểm của BCa) Chứng minh AI là tia phân giác góc Ab) Chứng minh AI vuông BCc) Kẻ IH vuông góc với AB (H thuộc AB), kẻ IK vuông góc với AB (K thuộcAC). Chứng minh IH = IK.d) Trên tia đối của tia IA lấy điểm D sao cho IA = ID. Chứng minh AB // CD
a) Xét ΔABI và ΔACI có
AB=AC(ΔABC cân tại A)
AI chung
BI=CI(I là trung điểm của BC)
Do đó: ΔABI=ΔACI(c-c-c)
nên \(\widehat{BAI}=\widehat{CAI}\)(hai góc tương ứng)
mà tia AI nằm giữa hai tia AB,AC
nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)
b) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: IB=IC(I là trung điểm của BC)
nên I nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AI là đường trung trực của BC
hay AI\(\perp\)BC(đpcm)
c) Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC(I là trung điểm của BC)
\(\widehat{HBI}=\widehat{KCI}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔIHB=ΔIKC(cạnh huyền-góc nhọn)
nên IH=IK(hai cạnh tương ứng)
d) Xét ΔABI vuông tại I và ΔDCI vuông tại I có
IB=IC(I là trung điểm của BC)
IA=ID(gt)
Do đó: ΔABI=ΔDCI(hai cạnh góc vuông)
nên \(\widehat{ABI}=\widehat{DCI}\)(hai góc tương ứng)
mà \(\widehat{ABI}\) và \(\widehat{DCI}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)
Đúng 2
Bình luận (0)
Cho đoạn thẳng BC . gọi I là trung điểm của BC , trên đường trung trực của đoạn BC lấy điểm A {A khác I }
a, CMR tam giác AIB = tam giác AIC
b, kẻ IH vuông góc với AB ,IK vuông góc với AC chứng minh IK=IH
c,qua C kẻ Cx song song với AB cắt AI kéo dài tại N . chứng minh CB là hân giác của góc ACN
Cho tam giác ABC vuông tại A , có góc C=30 độ. Gọi I là trung điểm BC kẻ IH vuông góc AC
a/ Cm: IH//AB
b/ Trên tia đối của IA lấy điểm K sao cho IK=IA . Cmr: tam giác ACK = tam giác ABC
Vẽ hình dùm mình nha
\(IH⊥AC\)
\(AB⊥AC\)
=> \(IH\)// AC
Câu này lười ghĩ wa
Phải chứng minh KC vuông góc AC
2 tam giác có AC chung 2 góc vuông thêm 1 dk nữa
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


















