Tìm nghiệm nguyên của hệ phương trình
2x-5y=5
2y-3z=1
Giải các hệ phương trình: 4 x 2 - 5 y + 1 = 2 x - 3 2 3 7 x + 2 = 5 2 y - 1 - 3 x
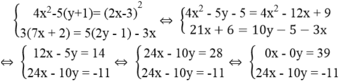
Vì phương trình 0x – 0y = 39 vô nghiệm nên hệ phương trình đã cho vô nghiệm.
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
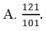
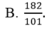
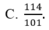
Hệ phương trình 2 x - 5 y + z = 10 x + 2 y - 3 z = 10 - x + 3 y + 2 z = - 16 có nghiệm là:
A. 2 ; - 2
B. - 2 ; 2 ; 4
C. 2 ; - 2 ; - 4
D. 2 ; - 1 ; 1
⇔ 2 x - 5 y + z = 10 x + 2 y - 3 z = 10 5 y - z = - 6 → ( 1 ) + ( 3 ) 2 x - 5 y + z = 10 x + 2 y - 3 z = 10 2 x = 4 ⇔ 4 - 5 y + z = 10 2 + 2 y - 3 z = 10 x = 2 ⇔ - 5 y + z = 6 2 y - 3 z = 8 x = 2 ⇔ - 15 y + 3 z = 18 2 y - 3 z = 8 x = 2 ⇔ - 13 y = 26 2 y - 3 z = 8 x = 2 ⇔ y = - 2 z = - 4 x = 2
Vậy nghiệm của hệ phương trình đã cho là ( 2; -2; -4).
Chọn C,
Tìm nghiệm nguyên của hệ \(\hept{\begin{cases}2x-5y=5\\2y-3z=1\end{cases}}\)
Hệ: \(\hept{\begin{cases}2x-5y=5\left(1\right)\\2y-3z=1\left(2\right)\end{cases}}\)
Từ \(\left(1\right)\Rightarrow y=\frac{2x-5}{5}\)
\(=\frac{2x}{5}-1\)(*)
Để \(y\inℤ\)thì \(\frac{2x}{5}-1\inℤ\)
\(\Leftrightarrow\frac{2x}{5}\inℤ\)
Nên \(2x⋮5\)
\(\Rightarrow2x=5k\) ( k là số nguyên khác 0 )
\(\Rightarrow x=\frac{5}{2}k\)
Vì vậy k phải chẵn để x nguyên
Thay \(x=\frac{5}{2}k\) vào (*) được
\(y=\frac{2}{5}.\frac{5}{2}k-1=k-1\)
Thay y = k - 1 vào (2) ta được
\(2k-2-3z=1\)
\(\Leftrightarrow2k-3z=3\)
\(\Leftrightarrow z=\frac{2}{3}k-1\)
Để \(z\inℤ\)thì \(\frac{2}{3}k-1\inℤ\)
\(\Leftrightarrow\frac{2}{3}k\inℤ\)
Nên 2k chia hết cho 3
\(\Rightarrow2k=3m\)(m là số nguyên khác 0 )
\(\Rightarrow k=\frac{3}{2}m\)
Nên m chẵn để k nguyên
=> m = 2n ( n nguyên khác 0)
=> k = 3n
Khi đó: \(z=\frac{2}{3}.3n-1=2n-1\)
Tổng hợp lại ta được
\(x=\frac{5}{2}k\) (i)
\(y=k-1\)
\(k=3n\)(n nguyên khác 0) (ii)
\(z=2n-1\)
Từ (i) và (ii) => n chẵn
=> n = 2q
\(\Rightarrow\hept{\begin{cases}x=\frac{5}{2}k=\frac{5}{2}.3n=\frac{5}{2}.3.2q=15q\\y=k-1=3n-1=3.2q-1=6q-1\\z=2n-1=2.2q-1=4q-1\end{cases}}\)
Vậy hệ có nghiệm nguyên \(\hept{\begin{cases}x=15q\\y=6q-1\\z=4q-1\end{cases}}\)(q là số nguyên khác 0)
P/S: mình thấy bài này không ổn lắm . Sai thì bạn thông cảm -.-
Tìm nghiệm nguyên của hệ pt: \(\hept{\begin{cases}2x-5y=5\\2y-3z=1\end{cases}}\)
GIÚP EM VỚI Ạ,EM CẦN GẤP Ạ
1)Cho phương trình 3x+2y=7.
Tìm nghiệm tổng quát của phương trình,tìm nghiệm nguyên của phương trình
2)Cho hệ phương trình: mx+y=1
4x+5y=3
Giải hệ phương trình với m= -2 bằng 2 cách (phương pháp thế,phương pháp cộng đại số)
Bài 1:
3x+2y=7
\(\Leftrightarrow3x=7-2y\)
\(\Leftrightarrow x=\dfrac{7-2y}{3}\)
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{7-2y}{3}\end{matrix}\right.\)
Tìm giá trị của m để nghiệm của hệ phương trình
x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x
cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
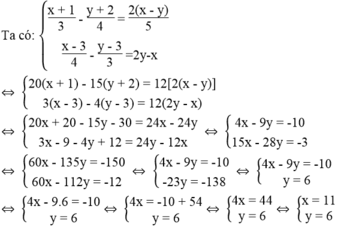
Vì (x; y) = (11; 6) là nghiệm của phương trình 3mx – 5y = 2m +1 nên ta có:
3m.11 – 5.6 = 2m + 1
⇔ 33m – 30 = 2m + 1 ⇔ 31m = 31 ⇔ m = 1
Vậy với m = 1 thì nghiệm của x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
GIẢI GIÚP MÌNH BÀI TOÁN NÀY ĐI Ạ!
Tìm nghiệm nguyên của hệ phương trình
\(\hept{\begin{cases}xy=x+y-z\\xz=2\left(x-y+z\right)\\yz=3\left(y-x+z\right)\end{cases}}\)
Tìm nghiệm nguyên dương của hệ phương trình
\(\hept{\begin{cases}x=5y+3\\x=11z+7\end{cases}}\)(x,y,z nhỏ nhất)
\(\hept{\begin{cases}x+2y+3z=20\\3x+5y+4z=37\end{cases}}\)(x,y,z nhỏ nhất)
LÀM GIÚP MÌNH Ạ!!! MAI MÌNH PHẢI KIỂM TRA RỒI!!!!
Tìm nghiệm nguyên của hệ phương trình
\(\hept{\begin{cases}xy=x+y-z\\xz=2\left(x-y+z\right)\\yz=3\left(y-x+z\right)\end{cases}}\)
Tìm nghiệm nguyên dương của hệ phương trình
\(\hept{\begin{cases}x=5y+3\\x=11z+7\end{cases}}\)(x,y,z nhỏ nhất)
\(\hept{\begin{cases}x+2y+3z=20\\3x+5y+4z=37\end{cases}}\)(x,y,z nhỏ nhất)
câu a)
nhân cả 3 phương trình
ta được
\(x^2y^2z^2=6\left(x+y-z\right)\left(x-y+z\right)\left(y-x+z\right)\)
Vế trái là 1 số chính phương nên Vp cũng là số chính phương
6 không phải là số chính phương nên
\(\left(x+y-z\right)\left(x-y+z\right)\left(y-x+z\right)\)=6
lập bảng
đặt x+y-z=1 ; x-y+z=2; y-x+z=3 giải ra và tương tự xét các cái còn lại (hơi lâu) nhớ xét thêm cái âm nữa
câu b)
từ hpt =>5y+3=11z+7
<=>\(y=\frac{11z+4}{5}\)>0 với mọi y;z thuộc R
y nguyên dương nên (11z+4)thuộc bội(5) và z_min
=> z=1
=> y=3
=> x =18 (t/m)
câu c)
qua pt (1) =>x=20-2y-3z
thay vao 2) <=> y+5z=23
y;z là nguyên dương mà 5z chia hêt cho 5
=> z={1;2;3;4}
=> y={18;13;8;3}
=> x={-19;-12;-5;2} đoạn này bạn làm từng GT của z nhé
chọn x=2; y=3; z=4 (t/m)
Nếu có sai sót hãy báo lại qua gmail: tiendung230103@gmail.com
Bạn giải nốt giùm mình câu a được ko?