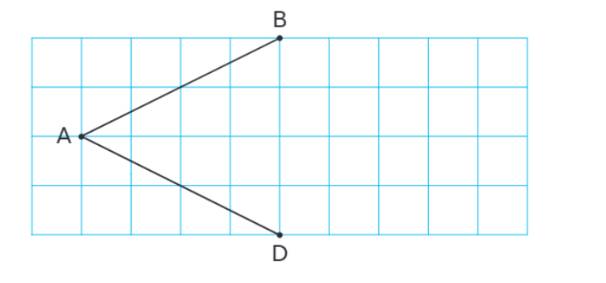
Xác định vị trí điểm C để có hình bình hành ABCD.
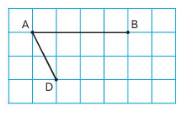
Cho ABCD là hình bình hành. Đường thẳng d đi qua A không cắt hình bình hành, ba điểm H, I, K lần lượt là hình chiếu của B, C, D trên đường thẳng d. Xác định vị trí đường thẳng d để tổng BH+CI+DK có GTLN.
Cho hình bình hành ABCD , trên AC lấy 2 điểm M và N sao cho AM = CN
a. Tứ giác BMND là hình gì ?
b. Hình bình hành ABCD phải thêm điều kiện gì thì BNDM là hình thoi
c. BM cắt AD tại K xác định vị trí của M để K là trung điểm của AD
d. Hình bình hành ABCD thỏa mãn cả 2 điều kiện ở b,c thì phải thêm điều kiện gì để BNDM là hình vuông
AB=CD,ˆBAM=ˆNCD,AB=CD→ΔAMB=ΔCND(c.g.c)→MB=DNAB=CD,BAM^=NCD^,AB=CD→ΔAMB=ΔCND(c.g.c)→MB=DN
→ˆAMB=ˆDNC→ˆBMN=ˆDNM→BM//DN→◊BNDM→AMB^=DNC^→BMN^=DNM^→BM//DN→◊BNDM là hình bình hành
b.Để ◊BNDM◊BNDM là hình thoi
→MN⊥BD→AC⊥BD→◊ABCD→MN⊥BD→AC⊥BD→◊ABCD là hình thoi
c.Để K là trung điểm AD →AK=KD→AK=KD mà KM//DN→MKM//DN→M là trung điểm AN →AM=MN=NC→AM=MN=NC

Cho hình thoi ABCD: AC=5,4cm; BD=6,8cm. Trên các cạnh AB, CD lần lượt lấy điểm M, N sao cho AMND là hình bình hành. Xác định vị trí điểm N để diện tích hình bình hành AMND=6,12 cm vuông.
Diện tích hình thoi ABCD là: 5,4 x 6,8 : 2 = 18,36 (cm2)
Diện tích hình thoi ABCD gấp diện tích hình bình hành AMND số lần là: 18,36 : 6,12 = 3 (lần)
⇒ PN = \(\dfrac{1}{3}\) PC
cho hình bình hành ABCD. qua A vẽ đường thẳng d không cắt hình bình hành. gọi B',C',D' lần lượt là hình chiếu vuông góc của các điểm B,C,D trên đường thẳng d. xác định vị trí cuả đường thẳng d để tổng BB'+CC'+DD' có giá trị nhỏ nhất
cho hình bình hành ABCD , trên đường chéo BD lấy điểm M và N sao cho BN = DM .
a) chứng minh tứ giác AMCN là hình bình hành
b) Hình bình hành ABCD có điều kiện gì để AMCN là hình thoi ?
c) gọi H là giao điểm AN và CD . Xác định vị trí của đỉnh N trên PD , để N là trung điểm của CD
( GIÚP MÌNH VỚI Ạ , MAI MÌNH ĐI HỌC RỒI Ạ )
cho hình bình hành ABCD, O là giao điểm 2 đg chéo. E thuộc OD, F là điểm đối xúng D qua E, xác định vị trí của E trên OD để tứ giác ODFA là hình bình hành
Cho ABCD là hình bình hành. Đường thẳng d đi qua A không cắt hình bình hành, ba
điểm H, I , K lần lượt là hình chiếu của B, C, D trên đường thẳng d. Xác định vị trí đường
thẳng d để tổng: BH + CI + DK có giá trị lớn nhất.

Gọi O là giao điểm hai đường chéo hình bình hành, kẻ OP \(\perp\) d\(\left(P\in d\right)\)
Ta có OP là đường trung bình của hình thang DKHB nên DK + BH = 2OP
Lại có OP là đường trung bình của \(\Delta ACI\) nên CI = 2OP
Do đó: DK + BH + CI = 4OP
Mà\(OP\le AO\)nên BH + CI + DK\(\le4OP\)
Dấu "=" xảy ra khi \(P\equiv A\)hay \(d\perp AC\)
Bạn vào đây có câu hỏi tương tự nhé :) Xem câu hỏi
Cho hình bình hành ABCD, trên BD lấy 2 điểm E và K sao cho BE = DK. Gọi O là giao điểm của AC và BD.
a, C/minh: OK = OE
b, C/minh: AK // EC
c, Tìm điều kiện của hình bình hành ABCD để AECK là hình thoi
d, Gọi M là giao điểm của AK và CD. Xác định vị trí điểm K để M là trung điểm CD.
Xác định vị trí điểm C để có hình thoi ABCD.