Tìm x trong mỗi tứ giác sau:
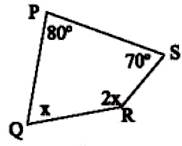
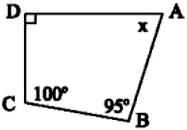
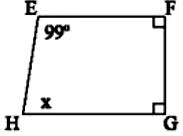
Tìm \(x\) trong mỗi tứ giác sau:
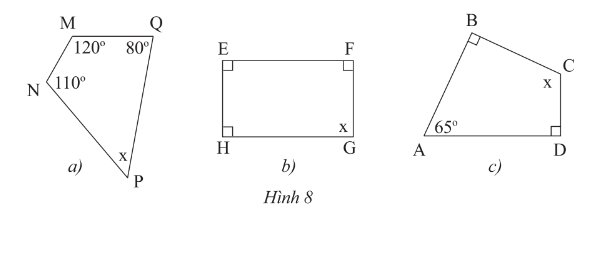
`a)`
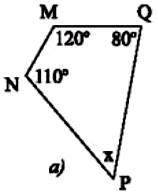
Xét tứ giác `MNPQ:`
$ \widehat {M} + \widehat {N} + \widehat {P} + \widehat {Q} = 360^0$
`=>` $120^0 + 110^0 + \widehat {P} + 80^0 = 360^0$
`=>`$ \widehat {P} = 50^0$
`=>` $x = \widehat {P}= 50^0$
Vậy, `x = 50^0`
`b)`
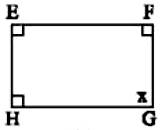
Xét tứ giác `EFGH:`
$\widehat {E} + \widehat {F} + \widehat {G} + \widehat {H} = 360^0$
`=>` $90^0 + 90^0 + \widehat {G} + 90^0 = 360^0$
`=>`$\widehat {G} = 90^0$
`=>` $x = \widehat {G} = 90^0$
Vậy, ` x= 90^0`
`c)`
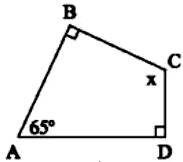
Xét tứ giác `ABCD:`
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D} = 360^0$
`=>` $65^0 + 90^0 + \widehat {C} + 90^0 = 360^0$
`=>` $\widehat {C} = 115^0$
`=>` $\widehat {C} = x = 115^0$
Vậy, `x = 115^0.`
a: x=360-120-80-110=50 độ
b: x=360-90-90-90=90 độ
c: x=360-90-90-65=115 độ
Tìm số đo x ở mỗi tứ giác sau:
a: Xét tứ giác MNPQ có
\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^0\)
=>\(x+80^0+110^0+120^0=360^0\)
=>\(x=50^0\)
b: Xét tứ giác EHGF có
\(\widehat{E}+\widehat{H}+\widehat{G}+\widehat{F}=90^0\)
=>\(x+90^0+90^0+90^0=360^0\)
=>\(x=90^0\)
c: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(x+90^0+90^0+65^0=360^0\)
=>\(x=115^0\)
Tìm 1 điểm trong tứ giác có thể chia tứ giác đó thành 4 phần có diện tích=nhau(mỗi phần là 1 tứ giác)
-help-
Tô màu vào hình tứ giác có trong mỗi hình vẽ sau:
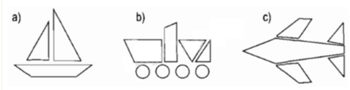
Phương pháp giải:
Tô màu các hình có bốn cạnh trong mỗi câu.
Lời giải chi tiết:
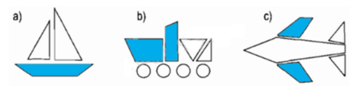
Tìm các hình tam giác và các hình tứ giác có trong hình sau:
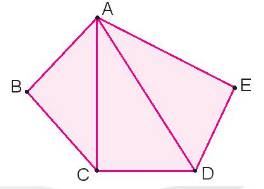
- Các hình tam giác là: ABC, ACD, ADE
- Các hình tứ giác là: ABCD, ACDE
Tô màu hình tứ giác có các cặp cạnh song song với nhau trong mỗi hình sau:
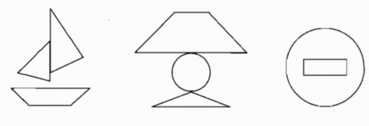
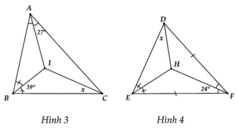
Tìm x trong mỗi hình vẽ sau biết I, H là giao điểm của ba đường phân giác của các góc trong của tam giác.
Kiểm đếm số chiếc diều mỗi loại trong hình vẽ sau (theo mẫu):
Số lượng chiếc diều mỗi loại
Chiếc diều có dạng khối hộp chữ nhật | 7 | |
Chiếc diều có dạng hình tứ giác | ? | ? |
Chiếc diều có dạng hình tam giác | ? | ? |
Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của mỗi tứ giác đối với mỗi đường thẳng đã vẽ.
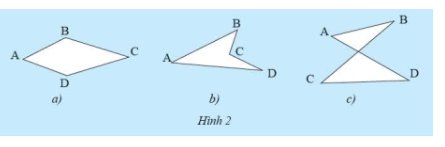
a: Các cạnh còn lại của tứ giác luôn nằm trong cùg một mặt phẳng
b: các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.
c: các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.