Gọi E, F lần lươt là trung điểm của AB và CD của hình bình hành ABCD. Chứng minh
a) AF// CE
b) Chứng minh AF và CE chia đường chéo BD thành 3 phần bằng nhau.
Những câu hỏi liên quan
Gọi E, F lần lươt là trung điểm của AB và CD của hình bình hành ABCD. Chứng minh
a) AF// CE
b) Chứng minh AF và CE chia đường chéo BD thành 3 phần bằng nhau.
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đo: AECF là hình bình hành
Suy ra: AF//CE
b: Gọi giao điểm của AF và EC với BD lần lượt là H,G
Xét ΔDGC có
F là trung điểm của DC
FH//GC
Do đó: H là trung điểm của DG
=>DH=HG(1)
Xét ΔAEB có
E là trung điểm của AB
EG//AH
Do đó: G là trung điểm của BH
=>BG=GH(2)
Từ (1) và (2) suy ra DH=HG=BG(đpcm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AB và CD. Nối AF và CE, 2 đường này cắt đường chéo BD lần lượt tại M và N. Chứng minh vectơ DM = vectơ MN = vectơ NB.
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy →DM=→MN=→NB
Đúng 0
Bình luận (0)
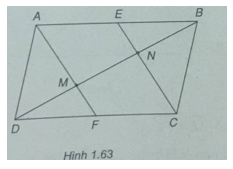
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AB và CD. Nối AF và CE, 2 đường này cắt đường chéo BD lần lượt tại M và N. Chứng minh vectơ DM = vectơ MN = vectơ NB.
xét tứ giác AECF: có AE = FC và AE//FC => AECF là hình bình hành => AF//CE
xét △DNC: có F là trung điểm của DC và FM//CN (đường tb) => M là trung điểm của DN => vtDM = vtMN (1)
xét △BMA: có E là trung điểm của AB và NE//AM ( đường tb) => N là trung điểm của MB => BM=MN (2)
từ (1) và (2) suy ra : DM=MN=NB => vtDM = vtMN = vtNB ( cùng hướng, cùng độ lớn)
Đúng 0
Bình luận (0)
Bài 1. Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD
a, Chứng minh rằng AF // CE
b, Gọi M, N theo thứ tự là giao điểm của BD với AF, CE. Chứng minh rằng DM = MN = NB
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD ( AB > AD). gọi AF là trung điểm của CD và AB . Đường chéo BD cắt AE, AC,CF lần lượt tạo N,O,M
a) chứng minh AECF là hình bình hành
b) chứng mính ba điểm B,E,F thẳng hàng
Lời giải:
a. Vì $ABCD$ là hình bình hành nên $AB=CD$
$\Rightarrow \frac{1}{2}AB=\frac{1}{2}CD$
$\Rightarrow AF=CE(1)$
Mặt khác: $AB\parallel CD\Rightarrow AF\parallel CE(2)$
Từ $(1); (2)\Rightarrow AECF$ là hình bình hành.
b.
B, E,F thẳng hàng??? Bạn xem lại đề.
Đúng 1
Bình luận (0)
Bài 10: Cho hình bình hành ABCD. Biết  = 1240.
a) Tính các góc của hình bình hành;
b) Gọi E, F lần lượt là trung điểm của AB và CD. Chứng minh: AF // CE;
c) Gọi O là trung điểm của AC. Chứng minh: E và F đối xứng nhau qua O.
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: FA//CE
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Đường chéo BD cắt AF ở G và cắt CE ở H. Chứng minh rằng:
a) DG=GH=HB. b) Các tứ giác AECF, EGFH, AGCH là các hình bình hành
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AD và BC. Đường chéo BD cắt AF và CE lần lượt tại M và N.
a) Chứng minh BM = MN = ND
b) Gọi I là trung điểm của CN. Chứng minh tứ giác DEMI là hình bình hành
Cho hình bình hành ABCD, gọi E, F lần lượt là trung điểm của AB và CD.a) Chứng minh AECF là hình bình hành b) AF và CE cắt BD lần lượt tại M và N, chứng minh
Đọc tiếp
Cho hình bình hành ABCD, gọi E, F lần lượt là trung điểm của AB và CD.
a) Chứng minh AECF là hình bình hành
b) AF và CE cắt BD lần lượt tại M và N, chứng minh
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Đúng 0
Bình luận (0)