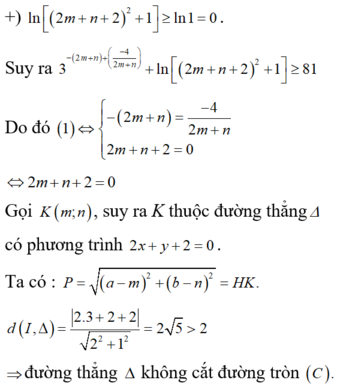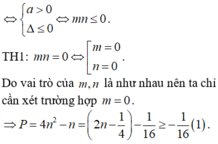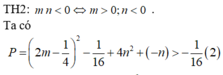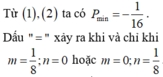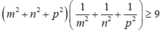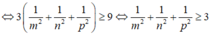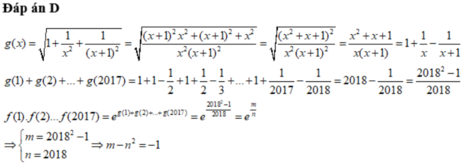Cho m, u là các số nguyên dương. Tìm giá trị chỏ nhất của vdk=m2+n2+1/m2+1/n2+2014

Những câu hỏi liên quan
1.Cho a,b,c là các số nguyên tố thoả mãn: ab + 1 = c. CMR: a2+ c hoặc b2+ c là số chính phương
2.Cho m,n là các số nguyên dương thoả mãn: m2+n2+m⋮mn. CMR: m là một số chính phương
Cho các số thực a, b, m, n sao cho
2
m
+
n
0
và thỏa mãn điều kiện
log
2
a
2
+
b
2
+...
Đọc tiếp
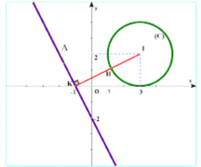
Cho các số thực a, b, m, n sao cho 2 m + n < 0 và thỏa mãn điều kiện log 2 a 2 + b 2 + 9 = 1 + log 2 3 a + 2 b 9 − m .3 − n .3 − 4 2 m + n + ln 2 m + n + 2 2 + 1 = 81
Tìm giá trị nhỏ nhất của biểu thức P = a − m 2 + b − n 2
A. 2 5 − 2.
B. 2.
C. 5 − 2.
D. 2 5 .
Cho m, n số nguyên dương, m2 + n2 + m chia hết cho mn. CMR m là số chính phương
Cho hàm số
f
(
x
)
x
3
-
(
m
2
+
m
+
1
)
x
+
m
2
+
m
có đồ thị cắt trục hoành tại ba điểm có hoành độ
x
1
,
x
2
,
x
3
. Biết m là s...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - ( m 2 + m + 1 ) x + m 2 + m có đồ thị cắt trục hoành tại ba điểm có hoành độ x 1 , x 2 , x 3 . Biết m là số nguyên dương, giá trị nhỏ nhất của biểu thức P = x 1 2 + x 2 2 + x 3 2 gần giá trị nào sau đây nhất
A. 2
B. 13/2
C. 6
D. 12
Hàm số
y
(
x
+
m
)
3
+
(
x
+
n
)
3
-
x
3
đồng biến trên khoảng
(...
Đọc tiếp
Hàm số y = ( x + m ) 3 + ( x + n ) 3 - x 3 đồng biến trên khoảng ( - ∞ ; + ∞ ) . Giá trị nhỏ nhất của biểu thức P = 4 ( m 2 + n 2 ) - m - n bằng
A. - 16
B. 4
C. - 1 16
D. 1 4
Trong không gian Oxyz, cho các điểm M(0;0;0), N(0;n;0), P(0;0;p) không trùng với gốc tọa độ và thỏa mãn
m
2
+
n
2
+
p
2
3
. Tìm giá trị lớn nhất của khoảng cách từ điểm O đến mặt phẳng (MNP) A.
1
3
B.
3
C.
1
3...
Đọc tiếp
Trong không gian Oxyz, cho các điểm M(0;0;0), N(0;n;0), P(0;0;p) không trùng với gốc tọa độ và thỏa mãn m 2 + n 2 + p 2 = 3 . Tìm giá trị lớn nhất của khoảng cách từ điểm O đến mặt phẳng (MNP)
A. 1 3
B. 3
C. 1 3
D. 1 27
Trong không gian Oxyz, cho các điểm
M
(
0
;
0
;
0
)
,
N
(
0
;
n
;
0
)
,
P
(
0
;
0
;
p
)
không trùng với gốc tọa độ và thỏa mãn
m
2
+
n
2
+
p
2...
Đọc tiếp
Trong không gian Oxyz, cho các điểm M ( 0 ; 0 ; 0 ) , N ( 0 ; n ; 0 ) , P ( 0 ; 0 ; p ) không trùng với gốc tọa độ và thỏa mãn m 2 + n 2 + p 2 = 3 . Tìm giá trị lớn nhất của khoảng cách từ điểm O đến mặt phẳng (MNP)
A . 1 3 .
B . 3 .
C . 1 3 .
D . 1 27 .
Cho hàm số
f
x
e
1
+
1
x
2
+
1
(
x
+
1
)
2
, biết rằn...
Đọc tiếp
Cho hàm số f x = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f 1 . f 2 . f 3 . . . f 2017 = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m 2 - n 2 .
A. m 2 - n 2 = 2018
B. m 2 - n 2 = 1
C. m 2 - n 2 = - 2018
D. m 2 - n 2 = - 1
Đồ thị hàm số y=x2 đi qua hai điểm (\(\sqrt{2}\);m)và(-\(\sqrt{3}\);n).Khi đó giá trị của biểu thức m2-n2 bằng
A.5 B.-1 C.1 D.-5
Thay hai điểm `(\sqrt{2};m)` và `(-\sqrt{3};n)` vào `y=x^2` ta có:
`{(m=(\sqrt{2})^2),(n=(-\sqrt{3})^2):}<=>{(m^2=4),(n^2=9):}`
`=>m^2-n^2=4-9=-5`
`->bb D`
Đúng 2
Bình luận (0)
Thay hai điểm vào hàm số
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{2}=m^2\\-\sqrt{3}=n^2\end{matrix}\right.\)
\(m^2-n^2=\sqrt{2}-\left(-\sqrt{3}\right)=\sqrt{2}+\sqrt{3}\)
Đúng 0
Bình luận (0)