Các câu hỏi tương tự
Cho hàm số yf(x) có đồ thị yf(x) cắt trục Ox hoành tại ba điểm có hoành độ -2ab như hình vẽ. Biết rằng f(-2)+f(1)f(a)+f(b). Để hàm số
y
f
(
x
+
m
)
có 7 điểm cực trị thì mệnh đề nào dưới đây là đúng A. f(a)0f(-2) B. f(-2)0f(a) C. f(b)0f(a) D. f(b)0f(-2)
Đọc tiếp
Cho hàm số y=f(x) có đồ thị y=f'(x) cắt trục Ox hoành tại ba điểm có hoành độ -2<a<b như hình vẽ. Biết rằng f(-2)+f(1)=f(a)+f(b). Để hàm số y = f ( x + m ) có 7 điểm cực trị thì mệnh đề nào dưới đây là đúng
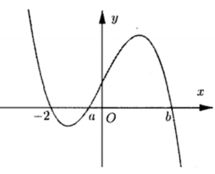
A. f(a)>0>f(-2)
B. f(-2)>0>f(a)
C. f(b)>0>f(a)
D. f(b)>0>f(-2)
Để đồ thị hàm số
(
C
)
:
y
x
3
-
2
x
2
+
(
1
-
m
)
x
+
m
(m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là
x
1
,
x
2
,
x
3...
Đọc tiếp
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
A. m < 1
B. m > 1 m < - 1 4
C. - 1 4 < m < 1
D. - 1 4 < m < 1 m ≠ 0
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số
y
x
3
+
(
m
+
2
)
x
2
+
(
m
2
-
m
-
3
)
x
-
m
2
cắt trục hoành tại ba điểm phân biệt A. 3 B. 2 C. 4 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 - m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt
A. 3
B. 2
C. 4
D. 1
Cho hàm số yf(x) có đồ thị là (C), hàm số yf(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,bGiá trị
(
a
-
b
)
2
thuộc khoảng nào dưới đây A.
(
0
;
9
)
B.
(
12
;
16
)
C.
(
16...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
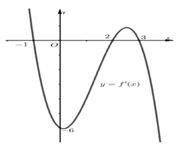
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Gọi M là điểm có hoành độ dương thuộc đồ thị hàm số
y
x
+
2
x
−
2
sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất. Tọa độ điểm M là A.
4
;
3
B.
0
;...
Đọc tiếp
Gọi M là điểm có hoành độ dương thuộc đồ thị hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất. Tọa độ điểm M là
A. 4 ; 3
B. 0 ; − 1
C. 1 ; − 3
D. 3 ; 5
Cho hàm số yf(x)(x-1) xác định và liên tục trên R và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng
y
m
2
-
m
cắt đồ thị hàm số
f
x
x
-
1
tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1] A.
m
0
B.
[
m...
Đọc tiếp
Cho hàm số y=f(x)(x-1) xác định và liên tục trên R và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m 2 - m cắt đồ thị hàm số f x x - 1 tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
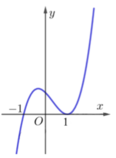
A. m > 0
B. [ m > 1 m < 0
C. m < 1
D. 0 < m < 1
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số
y
x
+
2
x
−
2
sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất. A. M(1;-3) B. M(3;5) C. M(0;-1) D. M(4;3)
Đọc tiếp
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất.
A. M(1;-3)
B. M(3;5)
C. M(0;-1)
D. M(4;3)
Cho hai hàm số đa thức bậc bốn yf(x)và yg(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số yf(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [-3;3] bằng A.
12
-
8
3
9
B. ...
Đọc tiếp
Cho hai hàm số đa thức bậc bốn y=f(x)và y=g(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y=f(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [-3;3] bằng
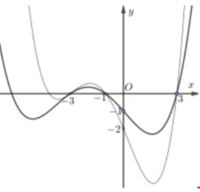
A. 12 - 8 3 9
B. - 3
C. 12 - 10 3 9
D. 10 - 9 3 9
Cho hàm số
y
x
3
-
2
(
m
+
1
)
x
2
+
(
5
m
+
1
)
x
-...
Đọc tiếp
Cho hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 có đồ thị là (Cm) với m là tham số. Có bao nhiêu giá trị của m nguyên trong đoạn [–10;100] để (Cm) cắt trục hoành tại ba điểm phân biệt A(2;0), B, C sao cho trong hai điểm B, C có một điểm nằm trong và một điểm nằm ngoài đường tròn có phương trình x2 + y2 = 1?
A. 109
B. 108
C. 18
D. 19




