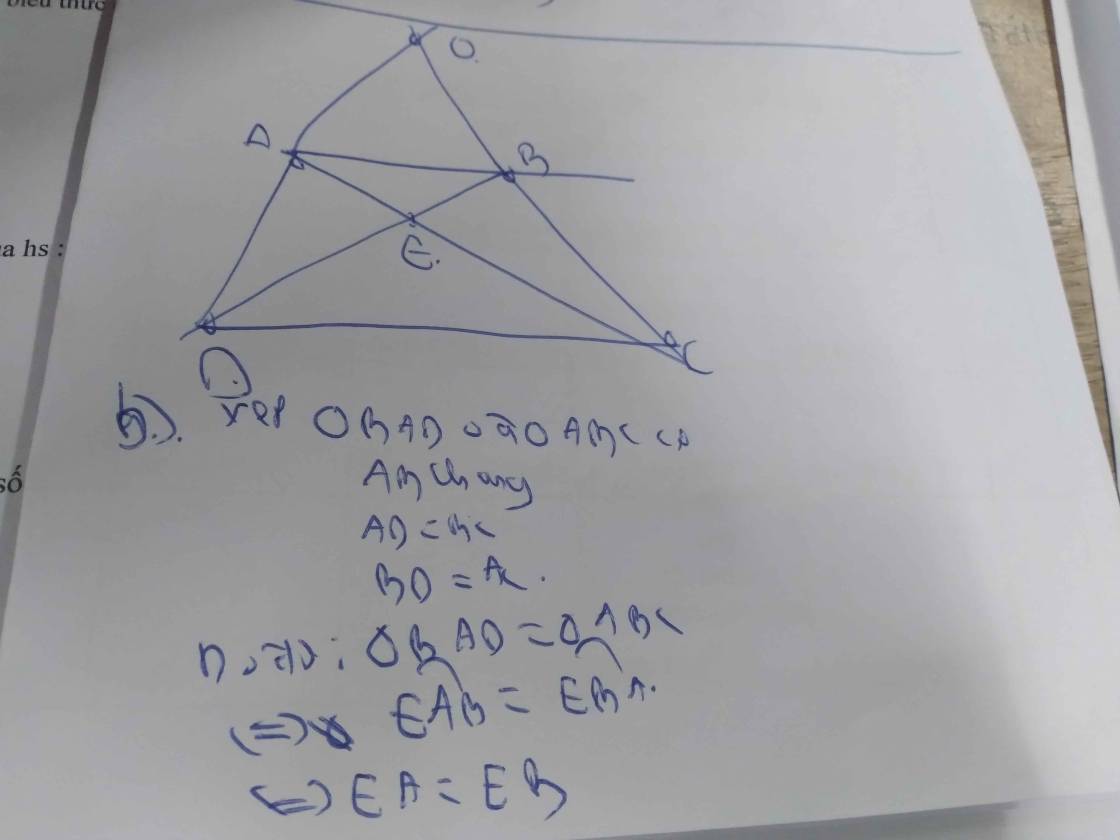
Cho hình thang cân ABCD (AB//CD) có AB < CD. Gọi O là giao điểm của AD và BC, E là giao điểm của AC và BD. C/m
a) Tam giác AOB cân
b) Tam giác ABD = tgiac BAC
c) EC = ED
d) OE là đường trung trực của AB và CD

Những câu hỏi liên quan
Bài 4
Cho hình thang cân ABCD (AB//CD,AB<CD)
Gọi {O} = AD giao BC; {E} = AC giao BD. Chứng minh:
a) Tam giác AOB cân tại O
b) Tam giác ABD = Tam giác BAC
c) EC = ED
d) OE là trung trực chung của AB và CD
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{OCD}=\widehat{ODC}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)
nên ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: Xét ΔACD và ΔBDC có
AC=BD
AD=BC
CD chung
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{EDC}=\widehat{ECD}\)
Xét ΔECD có \(\widehat{EDC}=\widehat{ECD}\)
nên ΔECD cân tại E
Đúng 1
Bình luận (0)
cho hình thang cân ABCD có AB ?? CD và AB < CD . Gọi O là giao điểm của AD và BC . E là giao điểm của AC và BD . CM
A) tam giác AOB cân tại O
B) tam giác ABD = tam giác BAC
C) EC = ED
D) OE là trung trực của hai đáy AB và CD
Cho hình thang cân ABCD (AB//CD, AB<CD). Gọi O là giao của AD và BC, gọi E là giao của AC và BD. CMR:
a) tam giác OAB cân
B) Tam giác ABD bằng tam giác BAC
C) EC=ED
D) OE là đường trung trực của AB và CD
a) Vì ABCD là hình thang cân
=> DAB = CBA
AD = BC
AC = BD
Ta có :
BAD + BAO = 180° ( kề bù )
CBA + ABO = 180° ( kề bù )
=> OAB = OBA
=> ∆OAB cân tại O
b) Xét ∆ABD và ∆BCA có :
AB chung
DAB = CBA (cmt)
AC = BD (cmt)
=> ∆ABD = ∆BCA (c.g.c)
c) Vì ∆ABD = ∆BCA
=> ADB = BCA
Xét ∆AED và ∆BEC có :
AD = BC
AED = BEC ( đối đỉnh )
ADB = BCD
=> ∆AED = ∆BEC (g.c.g)
=> DE = EC
d ) Vì ∆OAB cân tại O
=> OE là trung trực ∆OAB
Mà AB//CD ( ABCD là hình thang)
=> OE là trung trực CD
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có AB//CD , AB nhỏ hơn CD gọi O là giao điểm của AD và BC. E là giao điểm cua AC va BD
Cmr
Tam giác AOB cân tại O
Tam giác ABC = tam giác BAC
EC = ED
OE là trung trucchung của AB và CD
Mọi người ơi giúp mình bài này với.
Cho hình thang cân ABCD ( AB // CD ; AB < CD ) gọi O là giao điểm của 2 đường chéo AC và BD.
a) Chứng minh: tam giác AOB cân.
b) Chứng minh: OD = OC.
c) Gọi E là giao điểm AD và BC. Chứng minh: OE là trung trực của 2 đáy.
Cho hình thang cân ABCD có AB // CD và AB < CD. Kẻ đường cao AH, BK của hình thang ABCD (H, K thuộc CD).
1) Chứng minh tam giác ADH bằng tam giác BCK.
2) Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Chứng minh OI là trung trực của AB.
3) Giả sử BK=AB+CD/2. Tính góc tạo bởi hai đường chéo của hình thang.
Cho hình thang cân ABCD ( AB // CD ) . Gọi O là giao điểm của AC và BD ; E là giao điểm của AD và BC .
a ) Chứng minh : Tam giác OCD cân
b ) Chứng minh : EO là đường trung trực của : AB ; CD
a) Vì ABCD là hình thang cân
=> AD = BC
=> ADC = BCD
=> AC = BD
=> DAB = CBA
Xét ∆ADC và ∆BCD ta có :
AD = BC
ADC = BCD
DC chung
=> ∆ADC = ∆BCD (c.g.c)
=> BDC = ACD ( tương ứng)
=> ∆DOC cân tại O.
b) Mà DAB + BAE = 180° ( kề bù)
ABC + ABE = 180° ( kề bù )
Mà DAB = CBA
=> EAB = EBA
=> ∆EAB cân tại E
Gọi giao điểm AB và EO là H
EO và DC là G
Mà AB//CD
=> BAC = ACD ( so le trong)
=> ABD = ACD ( so le trong)
Mà ACD = BDC
=> CAB = ABD
=> ∆ABO cân tại O
=> EO là trung trực và là phân giác ∆AOB
=> AOH = BOH ( phân giác )
Mà AOH = COG ( đối đỉnh)
BOH = DOG ( đối đỉnh)
Mà AOH = BOH ( EO là phân giác)
=> OG là phân giác DOC
Mà ∆DOC cân tại O
=> OG là trung trực DC
Hay EO là trung trực DC
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có AB // CDvà AB CD. Kẻđường cao AH, BKcủa hình thang ABCD(H, K thuộc CD).1)Chứng minh tam giác ADH bằng tam giác BCK. 2)Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Chứng minh OI là trung trực của AB.3)Giảsử2ABCDBK+.Tính góc tạo bởi hai đường chéo của hình thang.
Đọc tiếp
Cho hình thang cân ABCD có AB // CDvà AB < CD. Kẻđường cao AH, BKcủa hình thang ABCD(H, K thuộc CD).1)Chứng minh tam giác ADH bằng tam giác BCK. 2)Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Chứng minh OI là trung trực của AB.3)Giảsử2ABCDBK+=.Tính góc tạo bởi hai đường chéo của hình thang.
Cho hình thang cân ABCD có AB // CDvà AB CD. Kẻđường cao AH, BKcủa hình thang ABCD(H, K thuộc CD).1)Chứng minh tam giác ADH bằng tam giác BCK. 2)Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Chứng minh OI là trung trực của AB.3)Giảsử BK(AB+CD)/2.Tính góc tạo bởi hai đường chéo của hình thang.
Đọc tiếp
Cho hình thang cân ABCD có AB // CDvà AB < CD. Kẻđường cao AH, BKcủa hình thang ABCD(H, K thuộc CD).
1)Chứng minh tam giác ADH bằng tam giác BCK.
2)Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Chứng minh OI là trung trực của AB.
3)Giảsử BK=(AB+CD)/2.Tính góc tạo bởi hai đường chéo của hình thang.
Tham khảo a làm rồi nha: https://hoc24.vn/cau-hoi/.1904701261424
Đúng 2
Bình luận (1)