tìm m để các hàm số sau là hàm bậc nhất:
a) y=(2m-1)x^2 + (m+1)x-3
b) (m^2+3m+7)x-2
Những câu hỏi liên quan
Cho hàm số bậc ba yf(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y|f(x)+m| có ba điểm cực trị là: A.
m
≤
-
1
hoặc
m
≥
3
B.
m
≤
-
3
hoặc
m
≥
1
C. m -1 hoặc m 3 D.
1
≤
m
≤
3
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
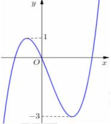
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
cho hàm số:
y = mx + 1 (1) (m là tham số)
a) Tìm m để đổ thị hàm số (1) đi qua A(1 ; 4) với giá trị m vừa tìm được hàm số (1) đồng biến hay nghịch biến
b) Tìm m để đô thị hàm số (1) // (d) y = m^2 x X + m + 1
Tìm m để hàm số sau nghịch biến:
a) y=(-m^2+2m-1)x-5
b)y=(m^2-m)x-1
c)y=3-(m^2+2m-3)x
cho hàm số y = 2x+2 có đồ thhij là (d) và hàm số y = -x-1 có đồ thị là (d1)
a, vẽ (d) và (d1) trên cùng 1 mặt phẳng tọa độ trên tọa độ giao điểm của (d) và (d1) bằng phép toán
b, cho hàm số y=(m^2-11) x+m-5 (m là hàm số) co đò thị là (d2).tìm m để đt (d2) cắt đt (d).tìm m dể đt (d2) song song với đường thẳng (d)
Tìm m để hàm số
y
-
x
3
+
(
2
m
+
1
)
x
2
-
(
m
2
-
3
m
+
2
)
x
-
4
có cực đại, cực tiểu nằm về hai phía so với trục tung A. m ∈ (1; 2) B. m ∈ [1; 2] C. m ∈ (- ∞; 1) ∪ (2; +∞) D. m ∈ (- ∞; 1] ∪ [2; +∞)
Đọc tiếp
Tìm m để hàm số y = - x 3 + ( 2 m + 1 ) x 2 - ( m 2 - 3 m + 2 ) x - 4 có cực đại, cực tiểu nằm về hai phía so với trục tung
A. m ∈ (1; 2)
B. m ∈ [1; 2]
C. m ∈ (- ∞; 1) ∪ (2; +∞)
D. m ∈ (- ∞; 1] ∪ [2; +∞)
y ' = - 3 x 2 + 2 ( 2 m + 1 ) x - m 2 + 3 m - 2
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm x 1 , x 2 trái dấu.
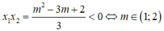
Chọn A
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y= (a+2)x-a+1 có đồ thị là đường thẳng (d) a) Tìm a để hàm số nghịch biến trên R; b) Tìm a để đường thẳng (d) đi qua điểm M(-1,-4)
Lời giải:
a. Để hàm số nghịch biến trên R thì:
$a+2<0$
$\Leftrightarrow a< -2$
b.
Để $(d)$ đi qua $M(-1;-4)$ thì:
$y_M=(a+2)x_M-a+1$
$\Leftrightarrow -4=(a+2)(-1)-a+1$
$\Leftrightarrow a=\frac{3}{2}$
Đúng 1
Bình luận (0)
Cho hàm số: y(m-1)x+m (d)a, Tìm m để hàm số đồng biến, nghịch biếnb, Tìm m để hàm số song song với trục hoànhc, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y1e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ x2-frac{sqrt{3}}{2}f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
Đọc tiếp
Cho hàm số: y=(m-1)x+m (d)
a, Tìm m để hàm số đồng biến, nghịch biến
b, Tìm m để hàm số song song với trục hoành
c, Tìm m để đồ thị hàm số đi qua điểm A(-1;1)
d, Tìm m để đồ thị hàm số song song với đường thẳng có phương trrình: x-2y=1
e, Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ \(x=2-\frac{\sqrt{3}}{2}\)
f, Chứng minh rằng đường thẳng (d) luôn đi qua điểm cố định khi m thay đổi
Cho hàm số
y
f
x
x
+
3
m
-
2
y. Tất cả các giá trị của tham số m sao cho
f
x
≥
0
,
∀
x
∈
[
1
;
+
∞
)
là A.
m
≤
1
3
B.
m
≤
2
3...
Đọc tiếp
Cho hàm số y = f x = x + 3 m - 2 y. Tất cả các giá trị của tham số m sao cho f x ≥ 0 , ∀ x ∈ [ 1 ; + ∞ ) là
A. m ≤ 1 3
B. m ≤ 2 3
C. m ≥ 1 3
D. 0 < m ≤ 2 3
Ta có f x ≥ 0 ⇔ x + 3 m ≥ 2 ⇔ x ≥ 2 - 3 m
f x ≥ 0 với mọi x ∈ [ 1 ; + ∞ ) ⇔ [ 1 ; + ∞ ) ⊂ [ 2 - 3 m ; + ∞ ) ⇔ 2 - 3 m ≤ 1 ⇔ m ≥ 1 3 .
Chọn C.
Đúng 0
Bình luận (0)
Câu 13: Tìm m để đồ thị hàm số f (x)=(m−1)x+2m+2 đi qua điểm A(1;4)
Thay x=1 và y=4 vào f(x), ta được:
m-1+2m+2=4
hay m=1
Đúng 0
Bình luận (0)