thế nào là hai góc kề nhau, cho ví dụ

Những câu hỏi liên quan
a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
b) Thế nào là tia phân giác của một góc?
c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau không? Hai góc so le trong có bằng nhau hay không?
e) Phát biểu tiên đề Euclid về đường thẳng song song.
a)
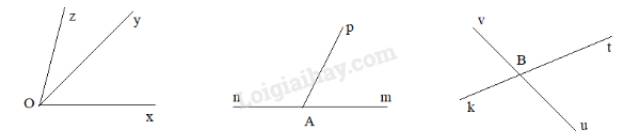
+ Ví dụ về 2 góc kề nhau: Góc xOy và góc yOz
+ Ví dụ về 2 góc kề bù: góc mAp và pAn
+ Ví dụ về hai góc đối đỉnh: góc uBt và góc vBk
b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
c)
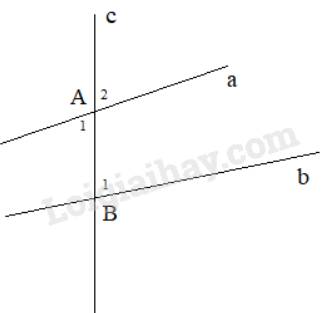
Đường thẳng c cắt hai đường thẳng a và b, tạo ra: Góc A1 và B1 là cặp góc so le trong; Góc A2 và B1 là cặp góc đồng vị
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau; hai góc so le trong bằng nhau ( Tính chất 2 đường thẳng song song)
e) Tiên đề Euclide về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
Đúng 0
Bình luận (0)
1. Số học1. Nêu quy tắc chuyển về, quy tắc dấu ngoặc? 2. Bội và ước của một số nguyên. 3. Viết dưới tổng quát của phân số. Cho ví dụ. 4. Nêu tính chất cơ bản của phân số bằng nhau? 5. Nêu tính chất cơ bản của phân số? Viết dưới dạng tổng quát. 6. Phát biểu quy tắc rút gọn phân số? Thế nào là phân số tối giản? Cho ví dụ. 7. Muốn so sánh hai phân số không dung mẫu số nhiều phân số? Cho ví dụ. 8. Phát biểu quy tắc quy đồng mẫu số nhiều phân số? Cho ví dụ. 9. Phát hiện và viết dạng tổng quát quy tắc...
Đọc tiếp
1. Số học
1. Nêu quy tắc chuyển về, quy tắc dấu ngoặc?
2. Bội và ước của một số nguyên.
3. Viết dưới tổng quát của phân số. Cho ví dụ.
4. Nêu tính chất cơ bản của phân số bằng nhau?
5. Nêu tính chất cơ bản của phân số? Viết dưới dạng tổng quát.
6. Phát biểu quy tắc rút gọn phân số? Thế nào là phân số tối giản? Cho ví dụ.
7. Muốn so sánh hai phân số không dung mẫu số nhiều phân số? Cho ví dụ.
8. Phát biểu quy tắc quy đồng mẫu số nhiều phân số? Cho ví dụ.
9. Phát hiện và viết dạng tổng quát quy tắc thực hiện các phép toán cộng, trừ, nhân, chia phân số?
10. Phát biểu tính chất cơ bản của phép cộng và phép nhân phân số.
a) Nêu quy tắc tìm giá trị phân số của một số cho trước? Cho ví dụ.
b) Nêu quy tắc tìm một số biết giá trị phân số của nó? Cho ví dụ.
c) Nêu cách tính tỷ số của hai số a và b? Tỷ số phần trăm? Cho ví dụ.
2. Hình học
11. Góc là hình như thế nào? Kí hiệu? Hình vẽ min họa.
12. Thế nào là góc vuông, góc nhọn, góc tù, góc bẹt?
13. Thế nào là hai góc phụ nhau; bù nhau; kề nhau, kề bù?
14. Khi nào thì xôy + yôz = xôz? Vẽ hình minh họa.
15. Thế nào là tia phân giác của một góc? Cách vẽ tai phân giác của một góc?
16. Tam giác ABC là hình như thé nào? Đường tròn (O; R) là hình như thế nào?
17. Nêu các cách chứng tỏ 1 tia nằm giữa hai tia? (đưa ra ví dụ minh họa)
thế nào là tia gốc o cho ví dụ .thế nào là hai tia đối nhau,trùng nhau,cho ví dụ
Cho ví dụ về hình ảnh hai góc kề nhau trong cuộc sống.
mình chỉ có ngần này ví dụ thôi mong bạn thông cảm:))
CHÚC BẠN HỌC TỐT!!!!!!!!!!!
Đúng 2
Bình luận (1)
Hai góc kề bù là gì?Cho ví dụ
Hai góc kề bù là hai góc kề nhau và có tổng số đo là 180⁰
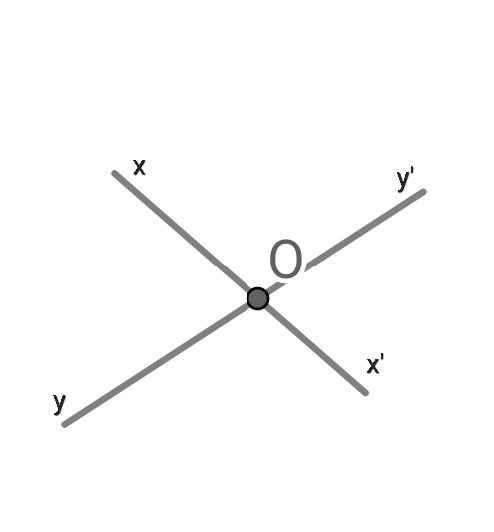
Trong hình trên, ∠xOy và ∠xOy' là hai góc kề bù
Đúng 2
Bình luận (0)
+ Hai góc kề bù là 2 góc vừa BÙ cho nhau và vừa KỀ cho nhau .
- Lý do hai góc kề bù có tổng số đo là 180 ĐỘ bởi vì hai góc bù nhau cũng có tổng số đo là 180 ĐỘ .
ngoài ra 2 góc kề bù cũng có thể có 1 cạnh trong chung nhưng không có điểm trong chung
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Nêu đặc điểm của hai góc kề nhau, phụ nhau,bù nhau, kề bù. Cho ví
dụ trong từng trường hợp (vẽ hình minh họa)
Xem chi tiết
dụ trong từng trường hợp (vẽ hình minh họa)
Góc bù nhau là 2 góc có tổng bằng 180 độ
Góc kề bù là hai góc kề nhau có tổng bằng 180 độ
Gó phụ nhau là có tổng hai góc bằng 90 độ
Góc kề nhau có tổng bằng 180 độ
và tổng hai góc phụ nhau bằng 90 độ
Xin lỗi nha ko vẽ được hình
k cho mk nha
Góc bù nhau là 2 góc có tổng bằng 180 độ
Góc kề bù là hai góc kề nhau có tổng bằng 180 độ
Gó phụ nhau là có tổng hai góc bằng 90 độ
Gó kề nhau có tổng bằng 180 độ
và tổng hai góc phụ nhau bằng 90 đô
cam on cac ban nha
Thế nào là hai góc kề bù?Thế nào là hai góc phụ nhau?Thế nào là hai gòc kề nhau?Thế nào là hai góc bù nhau?
Xem chi tiết
1) 2 góc kề bù là : hai góc vừa kề nhau vừa bù nhau
2) 2 góc phụ nhau là : là hai góc có tổng số đo = 90 độ, VD : góc 40 độ và góc 50 độ
3) 2 góc kề nhau là : hai góc hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung
4) 2 góc bù nhau là : hai góc có tổng số đo bằng 180 độ VD : góc 120 độ và góc 60 độ
Ủng hộ mik nha
Đúng 1
Bình luận (0)
Dễ mà, dở sách toán 6 kì 2 thì biết ngay.
Đúng 0
Bình luận (0)
1. Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nữa mặt phẳng đối nhau có bờ chứa cạnh chung.
VD:
2 Hai góc phụ nhau là hai góc có tổng số đo bằng \(^{90^o}\)
VD: góc 25 và góc 65.
4. Hai góc bù nhau là hai góc có tổng số đo bằng \(180^0\)
VD: góc 95 và góc 85.
3. Hai góc kề nhau là hai góc vừa kề nhau vừa bù nhau.
VD:
Đúng 0
Bình luận (0)
Hãy cho vài ví dụ (hình) về hai góc kề nhau.
Giúp mk với , thanks nhiều
Thế nào là hai hình bằng nhau, hai hình đồng dạng với nhau? Cho ví dụ.
+ Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Ví dụ: ΔABC sau khi thực hiện phép quay tâm C, góc 90º rồi lấy đối xứng qua d được ΔA1B1C1.
⇒ ΔABC = ΔA1B1C1
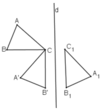
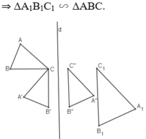
+ Hai hình được gọi là đồng dạng nếu có một phép đồng dạng biến hình này thành hình kia.
Ví dụ: ΔABC sau khi thực hiện liên tiếp phép quay tâm C góc 90º; đối xứng qua đường thẳng d và phép vị tự tâm B tỉ số 1,5 được ΔA1B1C1
Đúng 0
Bình luận (0)