Tính tổng \(C_{15}^{12} + C_{15}^{13} + C_{16}^{14}\)

Những câu hỏi liên quan
Tính:
a) \(C_7^2\)
b) \(C_9^0 + C_9^9\)
c) \(C_{15}^3 - C_{14}^3\)
a) \(C_7^2 = \frac{{7!}}{{2!.5!}} = \frac{{7.6}}{2} = 21\)
b) \(C_9^0 + C_9^9 = \frac{{9!}}{{0!.9!}} + \frac{{9!}}{{9!.0!}} = 2\)
c) \(C_{15}^3 - C_{14}^3 = \frac{{15!}}{{3!.12!}} - \frac{{14!}}{{3!.11!}} = \frac{{15.14.13}}{{3.2.1}} - \frac{{14.13.12}}{{3.2.1}} = 91\)
Đúng 0
Bình luận (0)
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau:
a) \(A_{15}^{10}\)
b) \(C_{10}^6 + C_{10}^7 + C_{11}^8\)
c) \(C_5^1C_{20}^2 + C_5^2C_{20}^1\)
a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
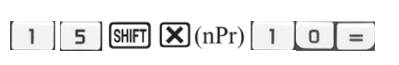
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím

Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím

Thì ta được kết quả là 1150
Đúng 0
Bình luận (0)
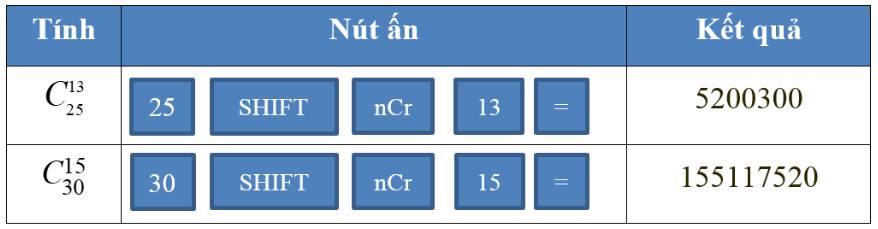
Dùng máy tính cầm tay để tính:
a)\(C_{25}^{13}\)
b)\(C_{30}^{25}\)
\(C_{14}^k+C_{14}^{k+2}=2C_{14}^{k+1}\)
\(C_{14}^k+C_{14}^{k+2}=2C_{14}^{k+1}\)
\(\Leftrightarrow\dfrac{14!}{\left(14-k\right)!k!}+\dfrac{14!}{\left(12-k\right)!\left(k+2\right)!}=\dfrac{2.14!}{\left(13-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\dfrac{14!}{k!\left(12-k\right)!}\left[\dfrac{1}{\left(14-k\right)\left(13-k\right)}+\dfrac{1}{\left(k+1\right)\left(k+2\right)}\right]=\dfrac{2}{\left(13-k\right)\left(k+1\right)}.\dfrac{14!}{k!\left(12-k\right)!}\)
\(\Leftrightarrow\dfrac{2k^2-24k+184}{\left(14-k\right)\left(k+2\right)\left(13-k\right)\left(k+1\right)}=\dfrac{2}{\left(13-k\right)\left(k+1\right)}\)
\(\Leftrightarrow\dfrac{k^2-12k+92}{-k^2+12k+28}=1\)
\(\Leftrightarrow k^2-12k+92=-k^2+12k+28\)
\(\Leftrightarrow k^2-12k+32=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=4\\k=8\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm giá trị của tổng \(S=C_{2017}^0+\dfrac{1}{2}C_{2017}^1+\dfrac{1}{3}C_{2017}^2+...+\dfrac{1}{2018}C_{2017}^{2017}\)
Xét khai triển:
\(\left(1+x\right)^{2017}=C_{2017}^0+xC_{2017}^1+x^2C_{2017}^2+...+x^{2017}C_{2017}^{2017}\)
Lấy tích phân 2 vế:
\(\int\limits^1_0\left(1+x\right)^{2017}=\int\limits^1_0\left(C_{2017}^0+xC_{2017}^1+...+x^{2017}C_{2017}^{2017}\right)\)
\(\Leftrightarrow\dfrac{2^{2018}-1}{2018}=C_{2017}^0+\dfrac{1}{2}C_{2017}^1+...+\dfrac{1}{2018}C_{2017}^{2017}\)
Vậy \(S=\dfrac{2^{2018}-1}{2018}\)
Đúng 0
Bình luận (0)
Tính F = \(2.1.C_{2021}^2+3.2.C_{2021}^3+...+k\left(k-1\right)C_{2021}^k+...+2021.2020.C_{2021}^{2021}\)
Tính tổng biểu thức sau: (sử dụng đẳng thức Niutơn)
A= \(C_{2n}^2\)+ \(C_{2n}^4\)+ \(C_{2n}^6\)+....+ \(C_{2n}^{2n}\)
\(B=C_{90}^0+2C_{90}^1+2^2C^2_{90}+....+2^{89}C_{90}^{89}+2^{90}C_{90}^{90}\) Tính B
Xét khai triển:
\(\left(1+x\right)^{90}=C_{90}^0+C_{90}^1x+C_{90}^2x^2+...+C_{90}^{90}x^{90}\)
Thay \(x=2\) ta được:
\(3^{90}=C_{90}^0+2C_{90}^1+2^2C_{90}^2+...+2^{90}C_{90}^{90}\)
Vậy \(B=3^{90}\)
Đúng 1
Bình luận (16)
Cho \(S=2015+C_{2016}^2+C_{2016}^3+C_{2016}^4+...+C_{2016}^{2016}\). Tìm S?
Gọi \(A=C_{2016}^0+C_{2016}^1+C_{2016}^2+...+C_{2016}^{2016}\)
\(=2^{2016}\) (HỆ QUẢ CỦA NHỊ THỨC NIUTON)
\(\Rightarrow\) \(S=2015+\left(A-C_{2016}^0-C_{2016}^1\right)\)
\(=2015+2^{2016}-1-2016\)
\(=2^{2016}-2\)
Đúng 0
Bình luận (0)