tam giác ABC,O nằm trong tam giác, OA cắt BC tại M, OB cắt AC tại N, OC cắt AB tại P.CMR (AM/OA)+(BN/OB)+(CP/OC) >=9/2

Những câu hỏi liên quan
tam giác ABC,O nằm trong tam giác, OA cắt BC tại M, OB cắt AC tại N, OC cắt AB tại P.CMR (AM/OA)+(BN/OB)+(CP/OC) >=9/2
Lấy một điểm O trong tam giác ABC. Các tia OA,OB,OC cắt BC,AC,AB lần lượt ở M,N,P chứng minh:
OA/AM+OB/BN+OC/CP=2
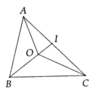
Cho tam giác ABC, điểm O nằm trong tam giác, tia BO cắt cạnh AC tại I. a) So sánh OA và IA + IO, từ đó suy ra OA + OB < IA + IB; b) Chứng minh: OA + OB < CA + CB; c) Chứng minh: (AB+AC+BC) /2 < OA + OB + OC < AB + BC + CA
Cho tam giác ABC có O là điểm nằm trong tam giác. Các tia AO, BO, CO cắt các cạnh đối diện tại M, N, P. Cmr:\(\frac{AM}{OA}.\frac{BN}{OB}.\frac{CP}{OC}\ge\frac{27}{8}\)
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 40^\circ \). Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó
A.\(OA = OB = AB\). B.\(OA = OB = OC\). C.\(OB = OC = BC\). D.\(OC = OA = AC\).
Đáp án: B. \(OA = OB = OC\).
Đúng 1
Bình luận (0)
Cho tam giác ABC điểm O nằm trong tam giác, tia BO cắt cạnh AC tại Ia) So sánh OA và IA + IO, từ đó suy ra OA + OB IA + IB;b) Chứng minh OA + OB CA + CB.c) Chứng minh
A
B
+
B
C
+
C
A
2
O
A
+
O
B
+
O...
Đọc tiếp
Cho tam giác ABC điểm O nằm trong tam giác, tia BO cắt cạnh AC tại I
a) So sánh OA và IA + IO, từ đó suy ra OA + OB < IA + IB;
b) Chứng minh OA + OB < CA + CB.
c) Chứng minh A B + B C + C A 2 < O A + O B + O C < A B + B C + C A
Lấy điểm O trong tam giác ABC. Các tia OA, OB, OC cắt BC; AC; AB lần lượt tại P; Q; R. Chứng minh OA/AP + OB/BQ + OC/CR = 2
Cho tam giác ABC , O nằm trong tam giác đó. Các tia AO,BO,CO cắt BC,CA,AB tại M,N,P. Chứng minh rằng:sqrt{frac{OA}{OM}}+sqrt{frac{OB}{ON}}+sqrt{frac{OC}{OP}}ge3sqrt{2}sqrt{frac{AM}{OA}}+sqrt{frac{BN}{OB}}+sqrt{frac{CP}{OC}}gefrac{3sqrt{6}}{2}sqrt{frac{OM}{AM}}+sqrt{frac{ON}{BN}}+sqrt{frac{OP}{CP}}gesqrt{3}Đã chứng minh:frac{AM}{OM}+frac{BN}{ON}+frac{CP}{OP}ge9frac{OA}{AM}+frac{OB}{ON}+frac{OC}{OP}ge6frac{AM}{OA}+frac{BN}{OB}+frac{CP}{OC}gefrac{9}{2}frac{OM}{OA}+frac{ON}{OB}+frac{OP}{OC}gefrac{...
Đọc tiếp
Cho tam giác ABC , O nằm trong tam giác đó. Các tia AO,BO,CO cắt BC,CA,AB tại M,N,P. Chứng minh rằng:
\(\sqrt{\frac{OA}{OM}}+\sqrt{\frac{OB}{ON}}+\sqrt{\frac{OC}{OP}}\ge3\sqrt{2}\)
\(\sqrt{\frac{AM}{OA}}+\sqrt{\frac{BN}{OB}}+\sqrt{\frac{CP}{OC}}\ge\frac{3\sqrt{6}}{2}\)
\(\sqrt{\frac{OM}{AM}}+\sqrt{\frac{ON}{BN}}+\sqrt{\frac{OP}{CP}}\ge\sqrt{3}\)
Đã chứng minh:
\(\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP}\ge9\)
\(\frac{OA}{AM}+\frac{OB}{ON}+\frac{OC}{OP}\ge6\)
\(\frac{AM}{OA}+\frac{BN}{OB}+\frac{CP}{OC}\ge\frac{9}{2}\)
\(\frac{OM}{OA}+\frac{ON}{OB}+\frac{OP}{OC}\ge\frac{3}{2}\)
( bài toán cực trị trong hình học).
a. Đặt \(S_{AOB}=c^2;S_{BOC}=a^2;S_{COA}=b^2\Rightarrow S_{ABC}=a^2+b^2+c^2\)
Ta có \(\frac{AM}{OM}=\frac{S_{ABC}}{S_{BOC}}=\frac{a^2+b^2+c^2}{a^2}=1+\frac{b^2+c^2}{a^2}\)
Vậy thì \(\frac{OA}{OM}=\frac{AM}{OM}-1=\frac{b^2+c^2}{a^2}\Rightarrow\sqrt{\frac{OA}{OM}}=\sqrt{\frac{b^2+c^2}{a^2}}\ge\frac{1}{\sqrt{2}}\left(\frac{b}{a}+\frac{a}{b}\right)\)
Tương tự, ta có: \(\sqrt{\frac{OA}{OM}}+\sqrt{\frac{OB}{ON}}+\sqrt{\frac{OC}{OP}}\ge\frac{1}{\sqrt{2}}\left(\frac{a}{b}+\frac{c}{b}+\frac{a}{c}+\frac{b}{c}+\frac{b}{a}+\frac{c}{a}\right)\ge\frac{1}{\sqrt{2}}.6=3\sqrt{2}\)
Đúng 0
Bình luận (0)











 tham khảo nha
tham khảo nha

