Tham khảo:

a) Áp dụng hệ quả của định lí cosin, ta có:

 \(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} =  - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)

\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.

b) 

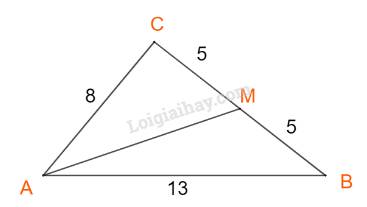
+) Áp dụng định lí cosin trong tam giác ACM, ta có:

\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)

+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).

Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)}  = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)}  \approx 40\)

+) Áp dụng định lí sin, ta có:

\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)

c) 

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)

Áp dụng định lí cosin trong tam giác BCD, ta có:

\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)

Gọi \(\widehat{A}:\widehat{B}:\widehat{C}\)lần lượt là a,b,c

Do \(\widehat{A}:\widehat{B}:\widehat{C}=3:4:5\)

\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}\)

Mà tổng \(\widehat{A}:\widehat{B}:\widehat{C}=180^o\)(tổng 3 góc trong tam giác)

=>\(\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)

\(\Rightarrow\hept{\begin{cases}\frac{a}{3}\\\frac{b}{4}\\\frac{c}{5}\end{cases}}=15\)

\(\Rightarrow\hept{\begin{cases}a=45^o\\b=60^o\\c=75^o\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}\widehat{A}=45^o\\\widehat{B}=60^o\\\widehat{C}=75^o\end{cases}}\)

MÀ \(\Delta ABC=\Delta A'B'C'\)

\(\Rightarrow\hept{\begin{cases}\widehat{A}=\widehat{A'}\\\widehat{B}=\widehat{B'}\\\widehat{C}=\widehat{C'}\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}\widehat{A'=45^o}\\\widehat{B'=60^o}\\\widehat{C'}=75^o\end{cases}}\)

Đặt: \(\widehat{A}=3x\Rightarrow\hept{\begin{cases}\widehat{B}=4x\\\widehat{C}=5x\end{cases}}\)

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow3x+4x+5x=180^o\)

\(\Rightarrow x=15\)

\(\Rightarrow\hept{\begin{cases}\widehat{A'}=\widehat{A}=3x=45^o\\\widehat{B}'=\widehat{B}=4x=60^o\\\widehat{C'}=\widehat{C}=75^o\end{cases}}\)

Vì \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}\) nên \(\widehat{A}-2\widehat{B}+\widehat{C}=0\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}-2\widehat{B}+\widehat{C}=0^0\left(1\right)\\\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(2\right)\end{matrix}\right.\)

Trừ \(\left(2\right)\) cho \(\left(1\right)\), ta được \(3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)

\(\Rightarrow\widehat{A}+\widehat{C}=120^0\)

Vậy GTLN của \(\widehat{A}\) là \(119^0\) vì \(\widehat{C}>0\)

$\widehat{ABC}$

Áp dụng định lí cosin trong tam giác ABC, ta có:

\(\begin{array}{l}{c^2} = {b^2} + {a^2} - 2ab\cos C\\ \Leftrightarrow {c^2} = 26,{4^2} + 49,{4^2} - 2.26,4.49,4\cos {47^ \circ }20'\\ \Rightarrow c \approx 37\end{array}\)

Áp dụng định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)

\(\begin{array}{l} \Leftrightarrow \frac{{49,4}}{{\sin A}} = \frac{{26,4}}{{\sin B}} = \frac{{37}}{{\sin {{47}^ \circ }20'}}\\ \Rightarrow \sin A = \frac{{49,4.\sin {{47}^ \circ }20'}}{{37}} \approx 0,982 \Rightarrow \widehat A \approx {79^ \circ }\\ \Rightarrow \widehat B \approx {180^ \circ } - {79^ \circ } - {47^ \circ }20' = {53^ \circ }40'\end{array}\)

Từ định lí cosin a² = b² + c² - 2bc. cosA

ta suy ra cos A = =

=> cosA ≈ 0,8089 => = 36⁰

Tương tự, ta tính được ≈ 106⁰ 28’ ; ≈ 37⁰ 32’.

a)

 

=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180^o

100^o + \(\widehat{B}+\widehat{C}\) = 180^o

\(\widehat{B}+\widehat{C}\) = 180^o - 100^o

\(\widehat{B}+\widehat{C}\) = 80^o

Góc B = (80^o+50^o):2 = 65^o

=> \(\widehat{C}\) = 65^o - 50^o = 15^o

Vậy \(\widehat{B}\) = 65^o ; \(\widehat{C}\) = 15^o

b)

 

Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180^o

\(\widehat{3A}+\widehat{2C}\) = 180^o - 80^o

\(\widehat{3A}+\widehat{2C}\) = 100^o

=> \(\widehat{A}\) = 100^o:(3+2).3 = 60^o

\(\widehat{C}\) = 100^o - 60^o = 40^o

Vậy \(\widehat{A}\) = 60^o ; \(\widehat{C}\) = 40^o

a) Áp dụng định lí cosin, ta có:

 \(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)

Áp dụng định lí sin, ta có:

\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)

b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)

c) 

+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)

+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)