cho hàm số y=(2m-5)x+m-1 và y=mx+3 tìm m để hai đồ thị đó song song với nhau

Những câu hỏi liên quan
Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5
Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
Hai đường thẳng song song với nhau.
Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
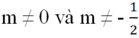
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
Đúng 0
Bình luận (0)
1. Cho hai hàm số bậc nhất y=mx+3 và y=(2m+1)x – 1.
Để đồ thị của hai hàm số đã cho là hai đường thẳng song song với nhau thì m = …
2. Cho hàm số y = ax+3. Để đồ thị hàm số song song với đường thẳng y = -5x thì a = …
\(1,\Leftrightarrow m=2m+1\Leftrightarrow m=-1\\ 2,\Leftrightarrow a=-5\)
Đúng 1
Bình luận (0)
Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5
Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
a) Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
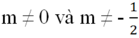
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:
m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có:
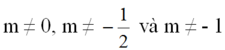
Đúng 1
Bình luận (0)
Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm m để đồ thị của các hàm số là: a) Hai đường thẳng song song với nhau. b) Hai đường thẳng cắt nhau. c) Hai đường thẳng vuông góc với nhau.
2 hàm số bậc nhất \(y=mx+3,y=\left(2m+1\right)x-5\left(đk:m\ne0,m\ne-\dfrac{1}{2}\right)\)
a) Để 2 đường thẳng song song với nhau thì:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=2m+1\\3\ne-5\left(luôn.đúng\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=-1\end{matrix}\right.\)
b) Để 2 đường thẳng cắt nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne2m+1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne-1\end{matrix}\right.\)
c) Để 2 đường thẳng vuông góc với nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\left(2m+1\right)=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\2m^2+m+1=0\left(VLý.do.2m^2+m+1=2\left(m+\dfrac{1}{4}\right)^2+\dfrac{7}{8}>0\right)\end{matrix}\right.\)
Vậy 2 đường thẳng này không vuông góc với nhau với mọi m
Đúng 1
Bình luận (0)
\(a,\Leftrightarrow\left\{{}\begin{matrix}m=2m+1\\-5\ne3\end{matrix}\right.\Leftrightarrow m=-1\\ b,\Leftrightarrow m\ne2m+1\Leftrightarrow m\ne-1\\ c,\Leftrightarrow m\left(2m+1\right)=-1\\ \Leftrightarrow2m^2+m+1=0\\ \Delta=1-8< 0\\ \Leftrightarrow m\in\varnothing\)
Vậy 2 đt không thể vuông góc nhau
Đúng 0
Bình luận (0)
a). Để hai hàm số bậc nhất song song với nhau thì:
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=2m+1\\3\ne-5\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m=-1\\3\ne-5\end{matrix}\right.\)
Vậy hai hàm số bậc nhất song song với nhau khi m=-1.
b). Để hai hàm số bậc nhất cắt nhau thì:
a≠a' ⇔ m ≠ 2m+1⇒m ≠ -1.
Vậy hai hàm số bậc nhất cắt nhau khi m ≠ -1.
c). chx hc
Đúng 1
Bình luận (0)
Cho hàm số y = mx + 4 và y = (2m - 3)x - 2. Tìm m để đồ thị của hai hàm số đãhị của hai hàm số làa, Hai đường thẳng cắt nhau, Hai đường thẳng song song với nhau , Hai đường thẳng trùng nhau
Cho hàm số y = mx + 4 và y = (2m - 3)x - 2. Tìm m để đồ thị của hai hàm sốđãhị của hai hàm số làa, Hai đường thẳng cắt nhau, Hai đường thẳng songsong với nhau , Hai đường thẳng trùng nhau
Đúng 0
Bình luận (0)
a: Để hai đường thẳng song song thì m=2m-3
hay m=3
Đúng 0
Bình luận (0)
Cho hai hàm số bậc nhất y = mx + 3 và y = (2m+1) x - 5. Tìm giá trị của m để đồ thị của hai hàm số đã cho là :
a) Hai đường thẳng song song với nhau
b) Hai đường thẳng cắt nhau
Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
1.Cho hai hàm số bậc nhất y=mx+3 và y=(2m -1) x-5. Tìm m để đồ thị của hai hàm số đã cho là
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau
c) Hai đường thẳng trùng nhau
giải chi tiết giúp mk vớiiii ạ
a: Để hai đường thẳng song song thì 2m-1=m
hay m=1
Đúng 1
Bình luận (1)
cho hàm số y=mx (1) (với m là tham số , m khác 0) a)Tìm m để đồ thị hàm số 1đi qua điểm M(-1;-1).Với m vừa tìm được ,vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy b)Tìm m để đồ thị hàm số (1) song song với đường thẳng (d):y+(m2-2)x+2m+3 c)Tìm m để khoảng cách từ gốc tọa độ O đến đồ thị hàm số (1) bằng 2/căn5
Cho hàm số bậc nhất \(y=mx+3\) và \(y=\left(2m+1\right)x-5\)
Tìm giá trị của m để đồ thị của hai hàm số đã cho là :
a) Hai đường thẳng song song với nhau
b) Hai đường thẳng cắt nhau
Cho hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau;
b) Hai đường thẳng cắt nhau.
Đúng 0
Bình luận (0)




















