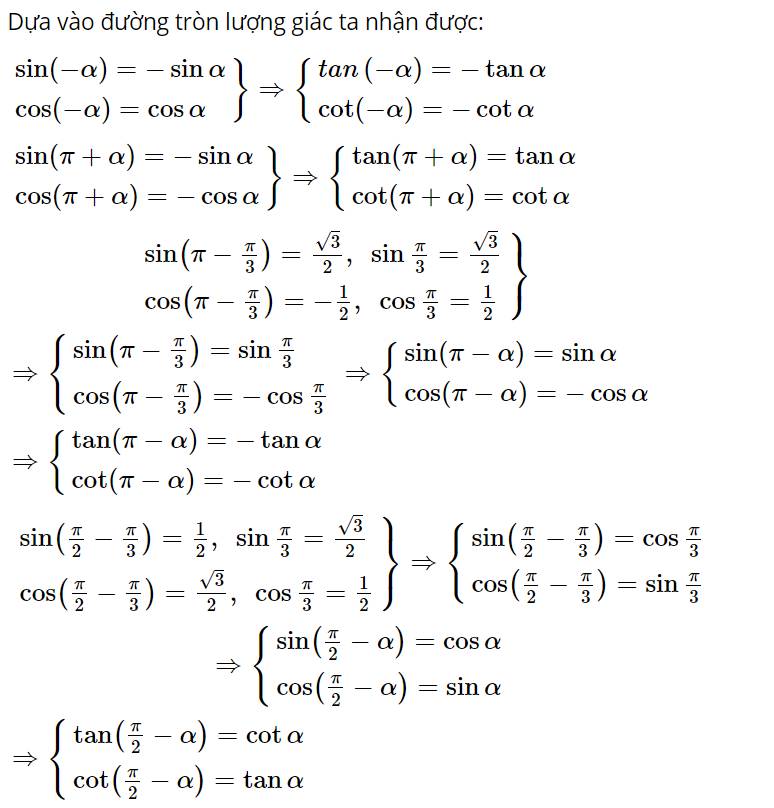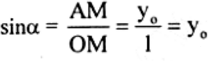Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)

Những câu hỏi liên quan
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = 45^\circ \)
\(\sin \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {45^\circ } \right) = \frac{1}{2};\,\,\cot \left( {45^\circ } \right) = 2\)
Đúng 0
Bình luận (0)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)
Đúng 0
Bình luận (0)
Nhắc lại khái niệm các giá trị lượng giác \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) của góc \(\alpha \)\(({0^ \circ } \le \alpha \le {180^ \circ })\) đã học ở lớp 10.
+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2).
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\)có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị nói trên để \(\widehat {xOM} = \alpha .\) Khi đó:
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)
Đúng 0
Bình luận (0)
Tính các giá trị lượng giác của góc α, nếu:
a) \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = \frac{2}{5}\) và \(0 < \alpha < 90^\circ \)
c) \(\tan \alpha = \sqrt 3 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
d) \(\cot \alpha = \frac{1}{2}\) và \(270^\circ < \alpha < 360^\circ \)
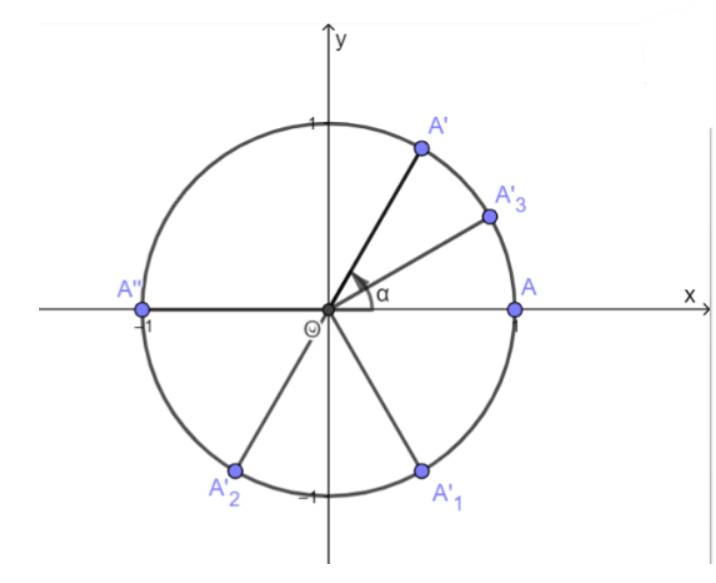
Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha + \pi ,\pi - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)
Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\) hoặc từ 0 đến \(45^\circ \) và tính
a) \(\cos \frac{{21\pi }}{6}\)
b) \(\sin \frac{{129\pi }}{4}\)
c) \(\tan 1020^\circ \)
\(a,cos\left(\dfrac{21\pi}{6}\right)=cos\left(3\pi+\dfrac{\pi}{2}\right)=cos\left(\pi+\dfrac{\pi}{2}\right)=-cos\left(\dfrac{\pi}{2}\right)=0\\ b,sin\left(\dfrac{129\pi}{4}\right)=sin\left(32\pi+\dfrac{\pi}{4}\right)=sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\\ c,tan\left(1020^o\right)=tan\left(5\cdot180^o+120^o\right)=tan\left(120^o\right)=-\sqrt{3}\)
Đúng 1
Bình luận (0)
a) Biểu diễn \(\cos 638^\circ \) qua gí trị lượng giác của góc có số đo từ \(0^\circ \) đến \(45^\circ \)
b) Biểu diễn \(\cot \frac{{19\pi }}{5}\) qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\)
a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)
b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)
Đúng 2
Bình luận (0)
Tính các giá trị lượng giác của mỗi góc sau: \(225^\circ ; - 225^\circ ; - 1035^\circ \);\(\frac{{5\pi }}{3};\frac{{19\pi }}{2}; - \frac{{159\pi }}{4}\)
\(\begin{array}{l}\cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \cos \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\sin \left( {{{225}^ \circ }} \right) = \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \sin \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\tan \left( {225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = 1\\\cot \left( {225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = 1\end{array}\)
\(\begin{array}{l}\cos \left( { - {{225}^ \circ }} \right) = \cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = - \cos \left( {{{45}^ \circ }} \right) = - \frac{{\sqrt 2 }}{2}\\\sin \left( { - {{225}^ \circ }} \right) = - \sin \left( {{{225}^ \circ }} \right) = - \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - 225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = - 1\\\cot \left( { - 225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = - 1\end{array}\)
\(\begin{array}{l}\cos \left( { - {{1035}^ \circ }} \right) = \cos \left( {{{1035}^ \circ }} \right) = \cos \left( {{{6.360}^ \circ } - {{45}^ \circ }} \right) = \cos \left( { - {{45}^ \circ }} \right) = \cos \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { - {{1035}^ \circ }} \right) = - \sin \left( {{{1035}^ \circ }} \right) = - \sin \left( {{{6.360}^ \circ } - {{45}^ \circ }} \right) = - \sin \left( { - {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - 1035^\circ } \right) = \frac{{\sin \left( { - {{1035}^ \circ }} \right)}}{{\cos \left( { - {{1035}^ \circ }} \right)}} = 1\\\cot \left( { - 1035^\circ } \right) = \frac{1}{{\tan \left( { - 1035^\circ } \right)}} = - 1\end{array}\)
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{3}} \right) = \cos \left( {\pi + \frac{{2\pi }}{3}} \right) = - \cos \left( {\frac{{2\pi }}{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{{5\pi }}{3}} \right) = \sin \left( {\pi + \frac{{2\pi }}{3}} \right) = - \sin \left( {\frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{{5\pi }}{3}} \right) = \frac{{\sin \left( {\frac{{5\pi }}{3}} \right)}}{{\cos \left( {\frac{{5\pi }}{3}} \right)}} = - \sqrt 3 \\\cot \left( {\frac{{5\pi }}{3}} \right) = \frac{1}{{\tan \left( {\frac{{5\pi }}{3}} \right)}} = - \frac{{\sqrt 3 }}{3}\end{array}\)
\(\begin{array}{l}\cos \left( {\frac{{19\pi }}{2}} \right) = \cos \left( {8\pi + \frac{{3\pi }}{2}} \right) = \cos \left( {\frac{{3\pi }}{2}} \right) = \cos \left( {\pi + \frac{\pi }{2}} \right) = - \cos \left( {\frac{\pi }{2}} \right) = 0\\\sin \left( {\frac{{19\pi }}{2}} \right) = \sin \left( {8\pi + \frac{{3\pi }}{2}} \right) = \sin \left( {\frac{{3\pi }}{2}} \right) = \sin \left( {\pi + \frac{\pi }{2}} \right) = - \sin \left( {\frac{\pi }{2}} \right) = - 1\\\tan \left( {\frac{{19\pi }}{2}} \right)\\\cot \left( {\frac{{19\pi }}{2}} \right) = \frac{{\cos \left( {\frac{{19\pi }}{2}} \right)}}{{\sin \left( {\frac{{19\pi }}{2}} \right)}} = 0\end{array}\)
\(\begin{array}{l}\cos \left( { - \frac{{159\pi }}{4}} \right) = \cos \left( {\frac{{159\pi }}{4}} \right) = \cos \left( {40.\pi - \frac{\pi }{4}} \right) = \cos \left( { - \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { - \frac{{159\pi }}{4}} \right) = - \sin \left( {\frac{{159\pi }}{4}} \right) = - \sin \left( {40.\pi - \frac{\pi }{4}} \right) = - \sin \left( { - \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { - \frac{{159\pi }}{4}} \right) = \frac{{\cos \left( { - \frac{{159\pi }}{4}} \right)}}{{\sin \left( { - \frac{{159\pi }}{4}} \right)}} = 1\\\cot \left( { - \frac{{159\pi }}{4}} \right) = \frac{1}{{\tan \left( { - \frac{{159\pi }}{4}} \right)}} = 1\end{array}\)
Đúng 0
Bình luận (0)
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc \(\alpha\) với \(0^0\le\alpha\le180^0\). Tại sao khi \(\alpha\) là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9 ?