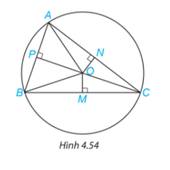
Vì A, B, C nằm trên đường tròn tâm O nên OA = OB = OC.

Xét hai tam giác ONA vuông tại N và ONC vuông tại N có:

        OA = OC (cmt)

        ON chung

Do đó  (cạnh huyền – cạnh góc vuông).

Xét hai tam giác OMB vuông tại M và OMC vuông tại M có:

        OB = OC (cmt)

        OM chung

Do đó  (cạnh huyền – cạnh góc vuông).

Xét hai tam giác OPA vuông tại P và OPB vuông tại P có:

        OA = OB (cmt)

        OP chung

Do đó  (cạnh huyền – cạnh góc vuông).

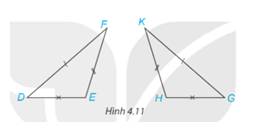
Ta có: Các cặp góc tương ứng là: \(\widehat E = \widehat H;\widehat D = \widehat G;\widehat F = \widehat K\)

Các cặp cạnh tương ứng là:\(ED=HG;EF=HK;DF=GK\)

Các cặp cạnh tương ứng : FE = KH , ED = HG , DF = GK

Các góc tương ứng : góc F = góc K, góc E = góc H, góc D = góc G

Kí hiệu bằng nhau của tam giác đó : ΔDFE=ΔGKH

a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:

AB=CD (gt)

\(\widehat {ABD} = \widehat {CDB}\) (gt)

BD chung

Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)

b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:

AO=CO (gt)

\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)

OD=OB (gt)

Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)

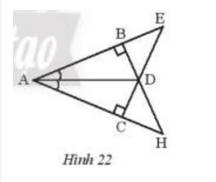
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:

AD chung

\(\widehat {BAD} = \widehat {DAC}\) (gt)

\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)

\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)

\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)

+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:

BD = CD (cmt)

\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )

\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )

+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)

                \(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)

Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)

\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)

Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:

\(\widehat {BAD} = \widehat {DAC}\) (gt)

AD chung

\(\widehat {ADE} = \widehat {ADH}\) (cmt)

\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )

+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:

AB = AC (cmt)

\(\widehat {BAH}\) chung

\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)

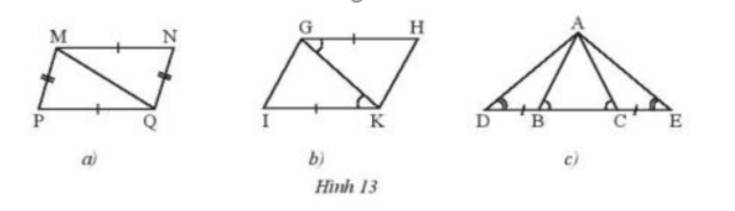
a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)

b) Ta thấy tam giác GHK  = tam giác GIK (c-g-c)

c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)

    Tam giác ADC = tam giác AEB (g-c-g)

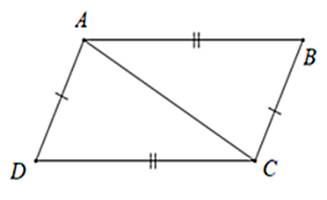
△ABC = △ADC (c.c.c) vì

AB = CD

AD = BC

AC chung

\(\Delta ABC=\Delta ADC\left(c.c.c\right)\)

Xét ΔABC và ΔADC có 

+AB=DC (GT)

+AD=BC (GT)

+AC là cạnh chung 

=> ΔABC=ΔADC (c.c.c)

ủa bn bắt đầu hút thuốc r hả?

các góc băng nhau:

ONTˆONT^ == NPKˆNPK^ (đồng vị)

NTOˆNTO^ == PITˆPIT^ (đồng vị)

IPOˆIPO^ == PORˆPOR^ (sole trong)

RONˆRON^ == ONTˆONT^ (sole trong)

-các góc bù nhau:

NTIˆNTI^ và NTOˆNTO^

-các góc ngòai của tam giác TNO:

TNPˆTNP^ ; ITNˆITN^

-tổng các góc trong của tứ giác PROI: 360o

-tổng các góc trong của tứ giác PNTI: 360o