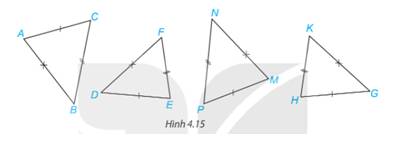
Trong Hình 4.15, những cặp tam giác nào bằng nhau?
cho hình tam giác ABCD ( AB và DC là đáy ) AC và AB gặp nhau ở M . hỏi trong hình đó có những cặp tam giác nào có diện tích bằng nhau
tự vẽ mình k biets vẽ hình kiểu gf cả , ở giấy rồi mình chỉ ở máy tính k biết giải kiểu gì
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
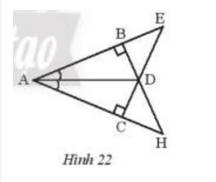
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
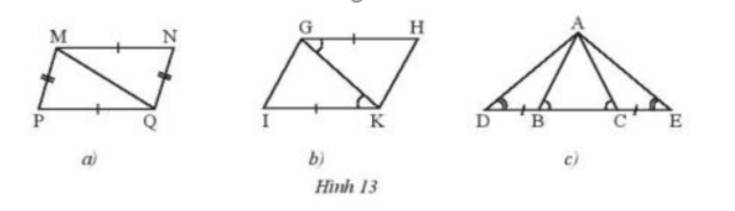
a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)
b) Ta thấy tam giác GHK = tam giác GIK (c-g-c)
c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)
Tam giác ADC = tam giác AEB (g-c-g)
Cho hình bên, trong đó ABCD là hình thang.
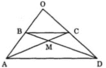
a, Trong hình thang đó những tam giác nào có diện tích bằng nhau? Vì sao?
b, Biết chiều cao của tam giác OBC kẻ từ O bằng chiều cao của hình thang ABCD. Hãy tìm trong hình thang đó xem những tam giác nào có diện tích bằng diện tích hình tam giác OBC. Vì sao?
a, Diện tích BAD = diện tích CAD (chung đáy AD, các đường cao vẽ từ B, C đến AD bằng nhau)
Diện tích ABC = diện tích BDC (chung đáy BC, các đường cao vẽ từ A và D đến BC bằng nhau)
Suy ra diện tích ABM bằng diện tích DCM
b, Diện tích ABC = diện tích DBC = diện tích OBC (chung đáy BC và 3 đường cao vẽ từ A, D, O đến BC bằng nhau)
Bài 8: Hãy chỉ ra các cặp tam giác bằng nhau trong và cho biết chúng bằng nhau theo trường hợp nào
Hình 1
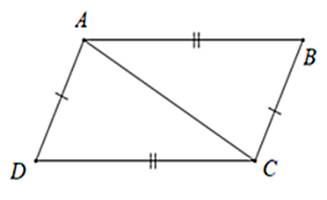
△ABC = △ADC (c.c.c) vì
AB = CD
AD = BC
AC chung
Xét ΔABC và ΔADC có
+AB=DC (GT)
+AD=BC (GT)
+AC là cạnh chung
=> ΔABC=ΔADC (c.c.c)
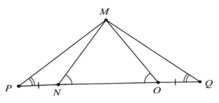
Có những tam giác nào bằng nhau trong hình bên? Vì sao?
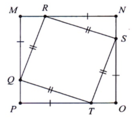
Cho hình vẽ với ABCD là hình vuông, tìm trong hình những tam giác nào bằng nhau.
Cho hình thang vuông ABCD. Hai đường chéo cắt nhau tại I. Điểm E nằm dưới cạnh DC, tam giác DEC có chiều cao bằng chiều cao hình thang.
A) Trong hình thang ABCD có những hình tam giác nào có diện tích bằng nhau?
B) Tìm những tam giác có diện tích bằng diện tích hình tam giác DEC