Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
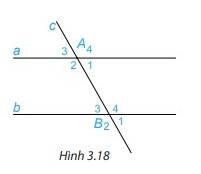
Trên Hình 3.18, cho biết hai góc so le trong A1 và B3 bằng nhau và bằng \(60^\circ \).
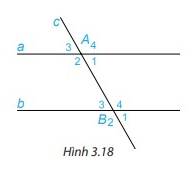
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Chọn cặp góc đồng vị: góc A1 và góc B4
Ta có: \(\widehat {{A_1}} = 60^\circ ;\widehat {{B_3}} = 60^\circ \)
\(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh)
\( \Rightarrow \widehat {{B_1}} = 60^\circ \)
Cho đoạn thẳng AB. Vẽ hai tia Ax, By sao cho chúng tạo với AB hai góc so le trong có cùng số đo bằng 60\(^\circ \)(\(\widehat {xAB} = \widehat {yBA} = 60^\circ \)). Trên hình vừa vẽ, hai đường thẳng chứa hai tia Ax và By có song song với nhau không? Vì sao?
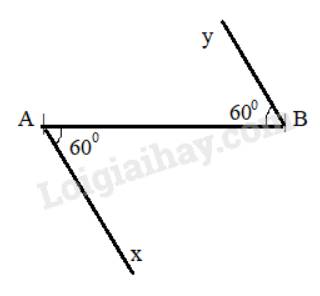
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
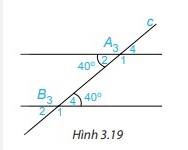
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
Cho hình vẽ biết 2 góc ở vị trí đòng vị A1=A2. Chứng tỏ :
a, Hai góc đồng vị còn lại bằng nhau
b, Hai góc trong cùng phía bù nhau
c, Hai góc so le trong bằng nhau
Cho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\).
a) Góc giữa hai đường thẳng \(MN\) và \(M'P\) bằng:
A. \({30^ \circ }\).
B. \({45^ \circ }\).
C. \({60^ \circ }\).
D. \({90^ \circ }\).
b) Gọi \(\alpha \) là số đo góc giữa đường thẳng \(M'P\) và mặt phẳng \(\left( {MNPQ} \right)\). Giá trị \(\tan \alpha \) bằng:
A. 1.
B. 2.
C. \(\sqrt 2 \).
D. \(\frac{1}{{\sqrt 2 }}\).
c) Số đo của góc nhị diện \(\left[ {N,MM',P} \right]\) bằng:
A. \({30^ \circ }\).
B. \({45^ \circ }\).
C. \({60^ \circ }\).
D. \({90^ \circ }\).
d) Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {NQQ'N'} \right)\) bằng:
A. \(a\).
B. \(\frac{a}{{\sqrt 2 }}\).
C. \(a\sqrt 2 \).
D. \(\frac{a}{2}\).
a) Đáp án:B
b) Đáp án:D
c) Đáp án:B
d) Đáp án:B
1. Vẽ 1 đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau và bằng 60 độ. Đặt tên cho các góc tạo thành đó .
a,Viết tên 1 cặp góc so le trong có số đo bằng 120 độ
b, Viết tên 1 cặp góc đồng vị có số đo bằng 60 độ
Giải giúp ạ, e cảm ơn !!
Cho 2 góc kề bù góc xOz và góc x'Oz biết góc xOz = 60 độ. Trên tia Oz lấy điểm I. Vẽ tia Iy' sao cho góc y'IO , góc xOI so le trong và bằng nhau. Vẽ tia đối Iy của tia Iy'
Tính góc yIO, góc yIz, góc y'Iz
a, Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau và bằng 60o . Đặt tên cho các góc tạo thành .
b, Viết tên một cặp góc so le trong có số đo bằng 120o
c, Viết tên một cặp góc đồng vị có số đo bằng 60o
a,
b, Vì đường thẳng c cắt đường thẳng a, b mà tạo thành 1 cặp góc so le trong bằng nhau
=> a//b
Ta có: B1 + B4 = 180o
=> B1 + 60o = 180o
=> B1 = 120o
Mà B1 = A3 (2 góc so le trong) => A3 = 120o
=> B1 và A3 là cặp góc so le trong có số đo bằng 120o
c, Vì a//b => B4 và A4 là 1 cặp góc đồng vị
=> B4 = A4 = 60o
Giúp mình bài hình này vs nha.. đang cần gấp ai tl đầu mik k nha
- Một đường thẳng c cắt cả hai đường thẳng song song a và b.
- Dùng thước đo góc, kiểm tra xem các góc đồng vị A1^ và B2^ có bằng nhau ko?
- Tương tự kiểm tra xem các góc so le trong A1^ và B1^ có bằng nhau ko?
Lưu ý: ^ là dấu mũ á nha mấy bạn
A 1 và B2 bằng nhau vì: theo định lý ( một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau )
A 1 và B1 bằng nhau vì theo định lý ( một đường thẳng cát hai đường thẳng song song thì hai góc so le trong bằng nhau )
Nói tóm gọm lại là bn chỉ trả lời hai góc này bằng nhau vì : theo đinh lý là xong
Mik học r
Bạn giải thích rõ cho mik vs đc hk.. tại cô kiểm tra cách làm đó bn.. mik k cho