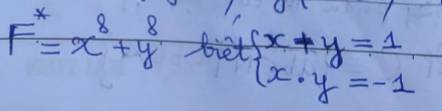
mọi người giúp e với ạ E cảm ơn
Mọi người giúp e câu 6 với những với, e đg cần gấp ạ. Cảm ơn mọi người ạ

mọi người giúp e với ạ, mai e kiểm tra rồi ạ, cảm ơn mọi người rất nhiều ạ !!
Mọi người giúp e câu này với ạ. E cảm ơn moinj người nhiều
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$
Mọi người giúp e bài này với ạ! e đag cần gấp! cảm ơn mọi người!
đâu cơ tôi chẳng hiểu?
giúp cho người ta học vẹt à?

Giúp e 2 câu a b với ạ e đang cần rất gấp e cảm ơn mọi người nhiều ạ!
a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)
Mọi người giúp e câu này với ạ em cảm ơn ạ

Mọi người giúp em đề này với ạ. E cảm ơn mọi người nhiều lắm
Mọi người giả giúp em với ạ e xin cảm ơn. chi tiết với ạ
b: ĐKXĐ: x>=2/3
PT=>(x-1)(x-2)+(x-1)*căn 3x-2=0
=>căn 3x-2+x-2=0
=>căn 3x-2=-x+2
=>x<=2 và 3x-2=x^2-4x+4
=>x^2-4x+4-3x+2=0 và x<=2
=>x=1
c: =>x+3+x-4-2căn (x^2-x-12)=1
=>2*căn x^2-x-12=2x-1-1=2x-2
=>căn x^2-x-12=x-1
=>x>=1 và x^2-x-12=x^2-2x+1
=>x=13
mọi người giúp e bài 5 ạ , e cảm ơn mọi người nhiều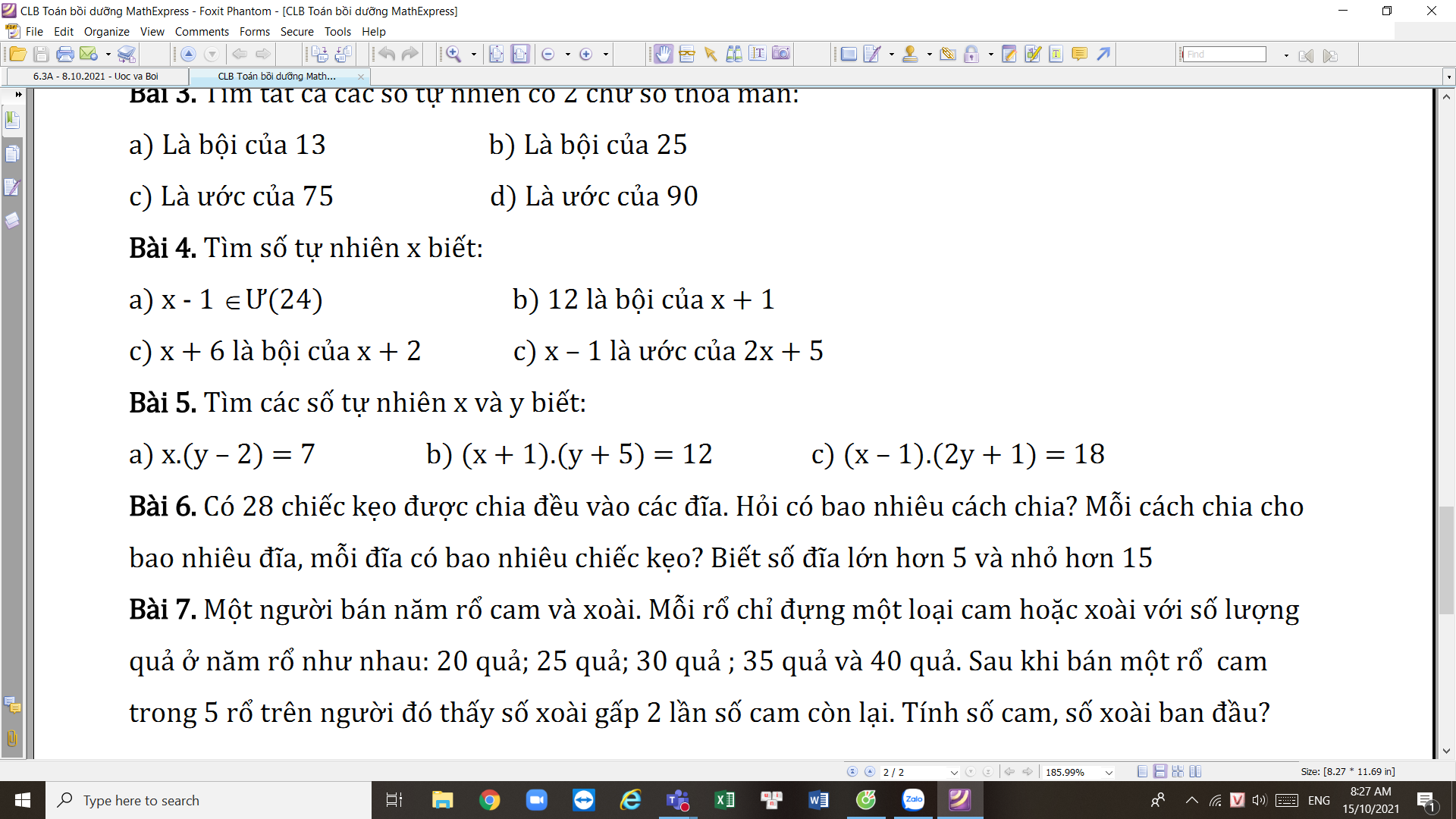
Bài 5:
a) Do \(x,y\in N\)
\(\Rightarrow\left\{\left(x;y-2\right)\right\}\in\left\{\left(1;7\right),\left(7;1\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;9\right),\left(7;3\right)\right\}\)
b) Do \(x,y\in N\)
\(\Rightarrow\left(x+1;y+5\right)\in\left\{\left(1;12\right),\left(2;6\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(0;7\right),\left(1;1\right)\right\}\)
c) Do \(x,y\in N\)
\(\Rightarrow\left(x-1;2y+1\right)\in\left\{\left(18;1\right),\left(2;9\right),\left(6;3\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(19;0\right),\left(3;4\right),\left(7;1\right)\right\}\)