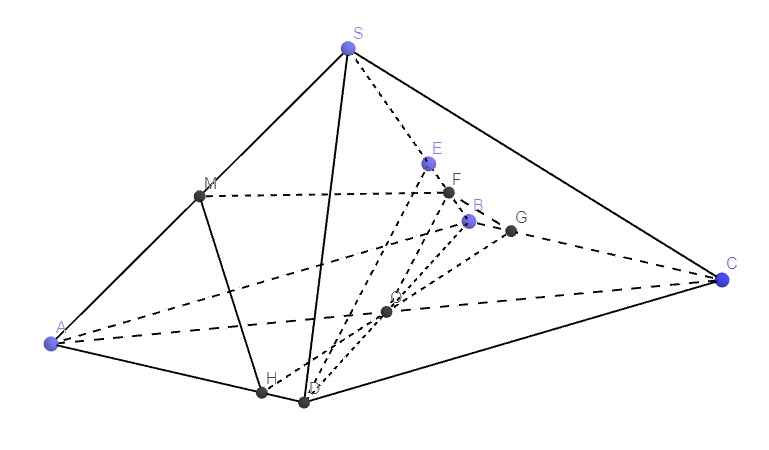
Cho hình chóp SABCD đáy là hình bình hành. M là trung điểm của SC. Tìm thiết diện của hình chóp với mp (ABM)

Những câu hỏi liên quan
Cho hình chóp SABCD có cạnh đáy không song song nhau . Gọi M là trung điểm SC . Tìm Thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM)
Xem chi tiết
Kéo dài AD và BC cắt nhau tại E
Trong mp (SBC), nối BM kéo dài cắt SE tại F
Trong mp (SAD), nối AF cắt SD tại P
\(\Rightarrow ABMP\) là thiết diện của (ABM) và chóp
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm thiết diện của (MAB) với hình chóp. A. thiết diện của (MAB) với hình chóp S.ABCD là tam giác MAB. B. thiết diện của (MAB) với hình chóp, S.ABCD là tứ giác ABMN, với N là giao điểm của SD với đường thẳng đi qua M và song song với AB. C. thiết diện của (MAB) với hình chóp S.ABCD là tứ giác ABMN, với N là giao điểm của MB và SD. D. thiết diện của (MAB) với hình chóp S.ABCD là tứ giác ABMN, với N là giao điểm của MA và SD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm thiết diện của (MAB) với hình chóp.
A. thiết diện của (MAB) với hình chóp S.ABCD là tam giác MAB.
B. thiết diện của (MAB) với hình chóp, S.ABCD là tứ giác ABMN, với N là giao điểm của SD với đường thẳng đi qua M và song song với AB.
C. thiết diện của (MAB) với hình chóp S.ABCD là tứ giác ABMN, với N là giao điểm của MB và SD.
D. thiết diện của (MAB) với hình chóp S.ABCD là tứ giác ABMN, với N là giao điểm của MA và SD.
Do (MAB) chứa AB // CD, nên giao tuyến của (MAB) với (SCD) là đường thẳng đi qua M và song song với AB. Đường thẳng này cắt SD tại điểm N.
Vậy thiết diện của (MAB) với hình chóp là tứ giác ABMN, với N là giao điểm của SD với đường thẳng đi qua M và song song với AB.
Đáp án B
Đúng 0
Bình luận (0)
cho hình chóp sabcd có đáy là hình bình hành abcd. m , n , e là trung điểm của ab , bc,sd. tìm thiết diện tạo bởi mặt phẳng mne và hình chóp
Trong mp (ABCD), nối MN kéo dài lần lượt cắt AD tại F và DC tại G
Trong mp (SAD), nối FE cắt SA tại P
Trong mp (SCD), nối EG cắt SC tại Q
\(\Rightarrow\) Ngũ giác MNQEP là thiết diện của (MNE) và chóp
Đúng 2
Bình luận (1)
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SA, E là điểm trên đoạn SB sao cho \(SE=\dfrac{2}{3}SB\). Thiết diện của mp đi qua M, song song với DE và SC với S.ABCD là hình gì?
Gọi (P) là mặt phẳng qua M, song song DE và SC
Gọi O là giao điểm AC, BD \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow\) OM là đường trung bình tam giác SAC
\(\Rightarrow OM||SC\Rightarrow O\in\left(P\right)\)
Trong mp (SBD), gọi F là trung điểm BE \(\Rightarrow OF\) là đường trung bình tam giác BDE
\(\Rightarrow OF||DE\Rightarrow F\in\left(P\right)\)
Trong mp (SBC), qua F kẻ đường thẳng song song SC cắt BC tại G
\(\Rightarrow G\in\left(P\right)\)
Trong mp (ABCD), nối GO kéo dài cắt AD tại H
\(\Rightarrow H\in\left(P\right)\)
\(\Rightarrow\) Thiết diện của (P) và chóp là tứ giác MFGH (và tứ giác này không có điều gì đặc biệt)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của các đoạn SB, SC, SA.
a) Tìm giao điểm giữa PN và (BDI), với I là trung điểm của NC
b) Tìm thiết diện hình chóp cắt bởi (CMP)
+ Chọn mp (SAC) chứa PN .
Ta có: - (SAC) giao ( BID) = I .
* I ∈ SC ⊂ (SAC).
* I ∈ ( BID).
Trong mp ( ABCD) có : AC cắt BD tại O .
=> Giao tuyến là OI.
Cho OI cắt PN tại đâu thì đấy là giao điểm.
Đúng 0
Bình luận (0)
Cho hình Chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi O là giao điểm của AC và BD
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SAB), (SAB)và (SCD)
b. Trên SC lấy điểm M tùy ý. Tìm giao điểm K của SD và mp (ABM)
c. Tìm thiết diện của hình chóp với mặt phẳng (ABM)
giúp mình với
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C’ là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mp(C’AE).
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE).
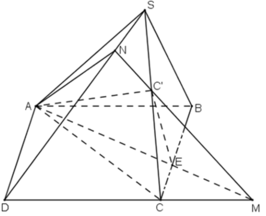
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy là hình thoi cạnh 3a,SA=SD=3a, SB=SC=\(3a\sqrt{3}\) . Gọi M,N lần lượt là trung điểm của các cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP=2a. Tinh diện tích thiết diện của hình chóp cắt bởi mp (MNP)
Lời giải:
Gọi $Q$ là điểm nằm trên $DC$ sao cho $AD\parallel PQ$
Khi đó: $MN\parallel AD\parallel PQ$ nên $Q\in (MNP)$
$(MNPQ)$ chính là thiết diện của hình chóp cắt bởi $(MNP)$
Giờ ta cần tìm diện tích hình thang $MNPQ$
$SA=SD; DB=SC; AB=CD$ nên $\triangle SAB=\triangle SDC$
Tương ứng ta có $MP=NQ$
$MN=\frac{AD}{2}=\frac{3a}{2}$
$PQ=AD=3a$
$\Rightarrow MNPQ$ là hình thang cân.
Áp dụng định lý cos:
$\cos \widehat{SAB}=\frac{SA^2+AB^2-SB^2}{2SA.AB}=\frac{MA^2+AP^2-MP^2}{2MA.AP}$
$\Leftrightarrow \frac{9a^2+9a^2-27a^2}{2.3a.3a}=\frac{\frac{9}{4}a^2+4a^2-MP^2}{2.\frac{3}{2}a.2a}$
$\Rightarrow MP^2=\frac{37}{4}a^2$
$\Rightarrow h_{MNPQ}=\sqrt{MP^2-(\frac{PQ-MN}{2})^2}=\frac{\sqrt{139}}{4}a$
Diện tích thiết diện:
$S=\frac{MN+PQ}{2}.h=\frac{9\sqrt{139}}{16}a^2$
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M,N là trung điểm SB,SC; lấy điểm P thuộc SA.
a. Tìm giao tuyến của (SAB) và (SCD)
b. Tìm giao điểm SD và (MNP)
c. Tìm thiết diện hình chóp và (MNP). Thiết diện là hình gì?