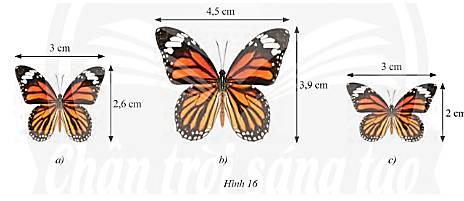
Trong các hình dưới đây, hai hình nào đồng dạng với nhau?
Người ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai hình tròn là 20 mét và 15 mét. Khoảng cách giữa hai tâm của hai hình tròn là 30 mét. Chi phí làm mỗi mét vuông phần giao của hai hình tròn là 300 nghìn đồng và chi phí làm mỗi mét vuông phần còn lại là 100 nghìn đồng. Hỏi số tiền làm mặt sân của sân khấu gần với số nào nhất trong các số dưới đây?
A. 208 triệu đồng
B. 202 triệu đồng
C. 200 triệu đồng
D. 218 triệu đồng
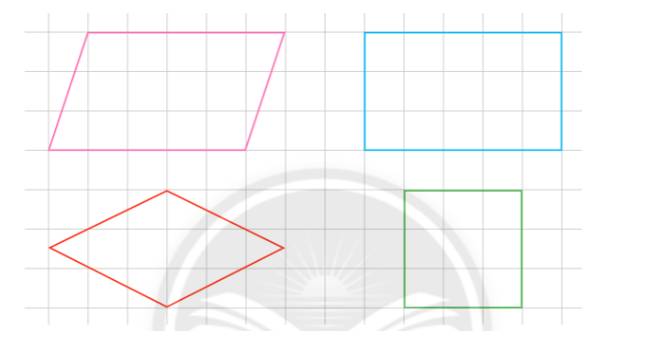
Quan sát các hình dưới đây rồi thực hiện các yêu cầu.
a) Gọi tên mỗi hình.
b) Trong các hình đã cho:
- Hình nào có hai cặp cạnh đối diện song song với nhau?
- Hình nào có bốn cạnh dài bằng nhau?
- Hình nào có bốn góc vuông?
Tham khảo:
a)
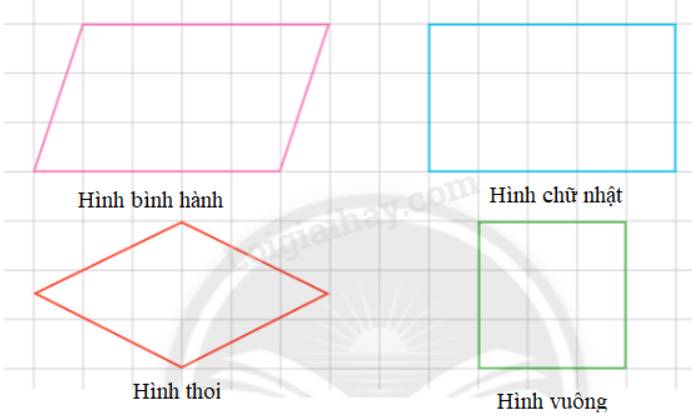
b)
– Hình có hai cặp cạnh đối diện song song với nhau là hình bình hành, hình chữ nhật, hình thoi, hình vuông.
- Hình có bốn cạnh dài bằng nhau là: Hình thoi, hình vuông
- Hình có bốn góc vuông là: Hình chữ nhật, hình vuông
Một khu vườn có dạng hợp của hai hình tròn giao nhau. Bán kính của hai đường tròn là 20m và 15m, khoảng cách giữa hai tâm của hai hình tròn là 30m. Phần giao của hai hình tròn được trồng hoa với chi phí 300000 đồng/ m 2 . Phần còn lại được trồng cỏ với chi phí 100000 đồng/ m 2 .Hỏi chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền nào dưới đây?
A. 202 triệu đồng.
B. 208 triệu đồng.
C. 192 triệu đồng.
D. 218 triệu đồng.
Đáp án A
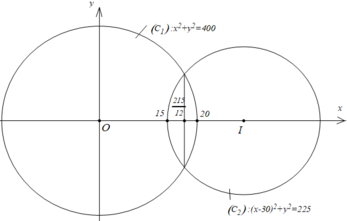
+ Gắn hệ trục như hình vẽ.
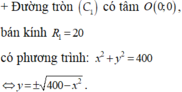
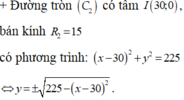
+ Phương trình hoành độ giao điểm của C 1 v à C 2 là
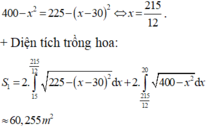

Vậy chi phí để trồng hoa và cỏ của khu vườn gần nhất với số tiền 202 triệu đồng
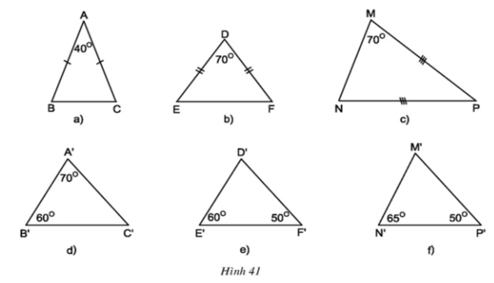
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
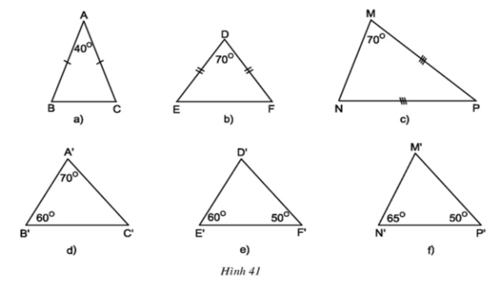
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Hai bóng đèn trong các mạch điện có sơ đồ nào dưới đây (hình 28.3) không mắc song song với nhau?
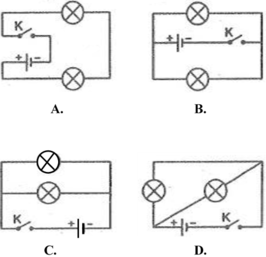
Đáp án: A
Trong hình 28.3 có sơ đồ mạch điện A là hai bóng đèn mắc nối tiếp nên không mắc song song với nhau.
Thế nào là hai hình bằng nhau, hai hình đồng dạng với nhau? Cho ví dụ.
+ Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
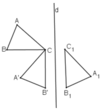
Ví dụ: ΔABC sau khi thực hiện phép quay tâm C, góc 90º rồi lấy đối xứng qua d được ΔA1B1C1.
⇒ ΔABC = ΔA1B1C1
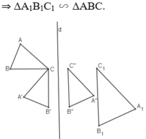
+ Hai hình được gọi là đồng dạng nếu có một phép đồng dạng biến hình này thành hình kia.
Ví dụ: ΔABC sau khi thực hiện liên tiếp phép quay tâm C góc 90º; đối xứng qua đường thẳng d và phép vị tự tâm B tỉ số 1,5 được ΔA1B1C1
Hợp thành của hai phép đối xứng qua hai đường thẳng cắt nhau là phép biến hình nào trong các phép biến hình dưới đây?
A. Phép đối xứng trục
B. Phép đối xứng tâm
C.Phép tịnh tiến
D. Phép quay
Trong hai mệnh đề sau đây, mệnh đề nào đúng? Mệnh đề nào sai?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác đồng dạng với nhau thì bằng nhau.
a) Mệnh đề Đúng.
Giả sử có ΔABC = ΔA’B’C’
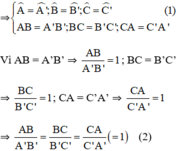
Từ (1) và (2) suy ra 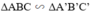
b) Mệnh đề Sai.
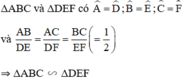
nhưng ΔABC và ΔDEF không bằng nhau
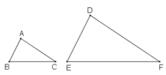
Thế nào là hai hình bằng nhau, hai hình đồng dạng với nhau ?
Cho ví dụ ?
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.
Định nghĩa:
Hai hình gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia.
Ví dụ:
Cho hình bình hành ABCD, khi đó một đường thẳng bất kỳ đi qua tâm O của ABCD, luôn chia hình bình hành ABCD ra thành hai hình bằng nhau.