cho đường tròn (o) đường kính AB và tiếp tuyến xAy , điểm M khác A trên xy , dây BN//OM
1) Chứng minh : OMlaf phân giác góc AON
2) Chứng minh : MN là tiếp tuyến của (o)

Những câu hỏi liên quan
Cho đường tròn (O) đường kính AB, tiếp tuyến xAy. Lấy điểm M trên xy, vẽ tiếp tuyến thứ hai MN (N là tiếp điểm).
a) Cm: dây BN // OM.
b) Đường thẳng vuông góc với AB tại O cắt đường thẳng BN tại K. Cm MK ⊥ xy.
c) Đường thẳng ON và MK cắt nhau tại S. Cm ∆OSM cân tại S.
a: Xét (O) có
MA,MN là tiếp tuyến
=>MA=MN
mà OA=ON
nên OM là đường trung trực của AN
=>OM\(\perp\)AN(1)
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
=>AN\(\perp\)NB(2)
Từ (1) và (2) suy ra OM//NB
b: Xét ΔMAO vuông tại A và ΔKOB vuông tại O có
AO=OB
\(\widehat{AOM}=\widehat{OBK}\)
Do đó: ΔMAO=ΔKOB
=>MA=KO
Xét tứ giác MAOK có
MA//OK
MA=OK
Do đó: MAOK là hình bình hành
mà \(\widehat{MAO}=90^0\)
nên MAOK là hình chữ nhật
=>KM\(\perp\)xy
Đúng 2
Bình luận (0)
cho đường tròn tâm (O;R) đường kính AB và điểm M trên đường tròn O sao cho góc MAB 60 độ. Kẻ dây MN vuông góc với AB tại H: 1. Chứng minh AM và AN là các tiếp tuyến của đường tròn (B;BM)2. Chứng minh MN2 4AH.HB3. Chứng minh tam giác BMN là tam giác đều và điểm O là trọng tâm của nó4. Tia MO cắt đường tròn (o) tại E, tia MB cắt (B) tại F. Chứng minh 3 điểm: N,E,F thẳng hàng.
Đọc tiếp
cho đường tròn tâm (O;R) đường kính AB và điểm M trên đường tròn O sao cho góc MAB= 60 độ. Kẻ dây MN vuông góc với AB tại H:
1. Chứng minh AM và AN là các tiếp tuyến của đường tròn (B;BM)2. Chứng minh MN2= 4AH.HB3. Chứng minh tam giác BMN là tam giác đều và điểm O là trọng tâm của nó4. Tia MO cắt đường tròn (o) tại E, tia MB cắt (B) tại F. Chứng minh 3 điểm: N,E,F thẳng hàng.1: ΔOMN cân tại O
mà OA vuông góc MN
nên OA là trung trực của MN
=>AM=AN
góc AMB=góc ANB=1/2*sđ cung AB=90 độ
Xét ΔAMB vuông tại M và ΔANB vuông tại N có
AB chung
AM=AN
=>ΔAMB=ΔANB
=>BM=BN
=>AM,AN là tiếp tuyến của (B;BM)
2: MH^2=AH*HB
=>4*MH^2=4*AH*HB
=>MN^2=4*AH*HB
3: góc MBA=90-60=30 độ
=>góc MBN=60 độ
=>ΔMBN đều
Đúng 0
Bình luận (0)
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC AMa) Chứng minh AB BCb) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyếnMC với đường tròn (C là tiếp điểm).a) Chứng minh OM // BCb) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hànhc) Chứng minh COMN là hình thang cân3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tu...
Đọc tiếp
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC = AM
a) Chứng minh AB = BC
b) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.
2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).
a) Chứng minh OM // BC
b) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hành
c) Chứng minh COMN là hình thang cân
3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).Kẻ CH vuông góc với AB tại H
a) Chứng minh CA là phân giác góc HCM
b) Kẻ CH vuông góc Ax tại K, gọi I là giao điểm của AC và HK. Chứng minh tam giác AIO vuông
c) Chứng minh 3 điểm M, I, O thẳng hàng
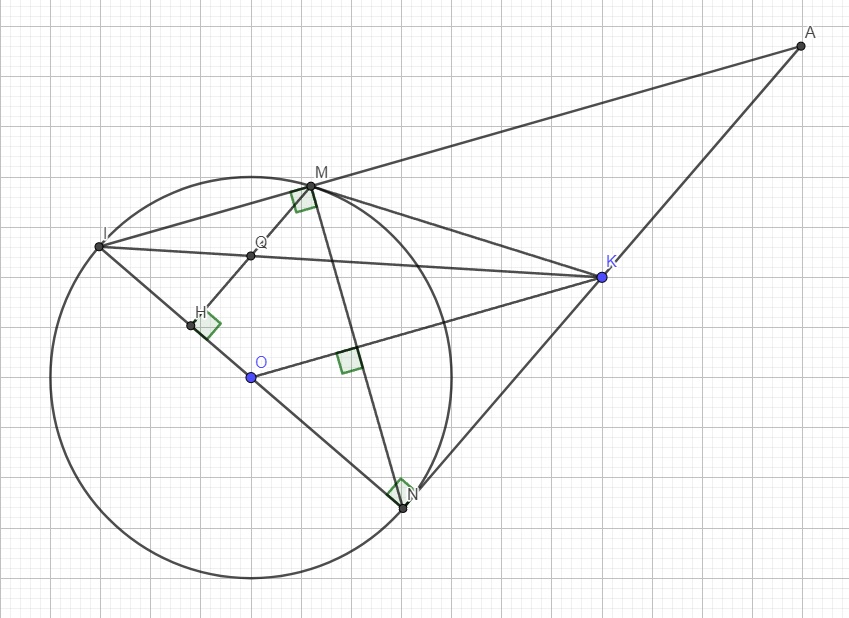
Cho đường tròn (O) đường kính AB, tiếp tuyến xAy. Lấy điểm M trên xy, vẽ tiếp tuyến thứ hai MN (N là tiếp điểm).
a) C/m dây BN//OM
b) Đường thẳng vuông góc với AB tại O cắt đường thẳng BN tại K. C/m MK ⊥ xy.
c) Đường thẳng ON và MK cắt nhau tại S. C/m ∆OSM cân tại S
a) Để chứng minh dây BN // OM, ta sử dụng định lý góc tiếp tuyến: Góc NAB = Góc NMB (do AB là tiếp tuyến). Vì OM là đường phân giác góc NMB, nên góc NMO = góc NMB/2. Tương tự, góc BON = góc BAN = góc NMB/2. Do đó, góc NMO = góc BON, suy ra dây BN // OM. b) Đường thẳng vuông góc với AB tại O là đường phân giác góc AOB. Vì MK là đường phân giác góc AMB, nên góc AMK = góc BMO = góc AOB/2. Vì đường thẳng vuông góc với AB tại O cắt đường thẳng BN tại K, nên góc BKO = góc AOB/2. Do đó, góc AMK = góc BKO, suy ra MK ⊥ xy. c) Đường thẳng ON và MK cắt nhau tại S. Vì ON là đường phân giác góc AOB, nên góc ONS = góc OAS = góc AOB/2. Vì MK là đường phân giác góc AMB, nên góc MSK = góc MAK = góc AOB/2. Do đó, góc ONS = góc MSK, suy ra ∆OSM cân tại S....
Đúng 0
Bình luận (1)
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Cho đường tròn (O) đường kính AB. Lấy điểm M thuộc (O) sao cho MA MB. Vẽ dây MN vuông góc với AB tại H. Đường thẳng AN cắt BM tại C. Đường thẳng qua C vuông góc với AB tại K và cắt BN tại Da, Chứng minh A, M, C, K cùng thuộc đường trònb, Chứng minh BK là tia phân giác của góc MBNc, Chứng minh ∆KMC cân và KM là tiếp tuyến của (O)d, Tìm vị trí của M trên (O) để tứ giác MNKC trở thành hình thoi
Đọc tiếp
Cho đường tròn (O) đường kính AB. Lấy điểm M thuộc (O) sao cho MA < MB. Vẽ dây MN vuông góc với AB tại H. Đường thẳng AN cắt BM tại C. Đường thẳng qua C vuông góc với AB tại K và cắt BN tại D
a, Chứng minh A, M, C, K cùng thuộc đường tròn
b, Chứng minh BK là tia phân giác của góc MBN
c, Chứng minh ∆KMC cân và KM là tiếp tuyến của (O)
d, Tìm vị trí của M trên (O) để tứ giác MNKC trở thành hình thoi

a, C K A ^ = C M A ^ = 90 0 => C, K, A, M thuộc đường tròn đường kính AC
b, ∆MBN cân tại B có BA là đường cao, trung tuyến và phân giác
c, ∆BCD có BK ⊥ CD và CN ⊥ BN nên A là trực tâm của ∆BCD => D,A,M thảng hàng
Ta có ∆DMC vuông tại M có MK là trung tuyến nên ∆KMC cân tại K
=> K C M ^ = K M C ^
Lại có K B C ^ = O M B ^ nên
K M C ^ + O M B ^ = K C B ^ + K B C ^ = 90 0
Vậy K M O ^ = 90 0 mà OM là bán kính nên KM là tiếp tuyến của (O)
d, MNKC là hình thoi
<=> MN = CK và CM = CK
<=> ∆KCM cân
<=> K B C ^ = 30 0 <=> AM = R
Đúng 0
Bình luận (1)
DM cũng là đường cao nên CN cũng thế thôi :)))
à không:)) t nghĩ là tam giác anb nội tiếp đường tròn đk ab nên nó vuông tại n:)))
cho đường tròn ( O ; R ) dây MN khác đường kính. Qua O kẻ đường vuông góc với MN tại H , cắt tiếp tuyến tại M của đường tròn (O).
1. Chứng minh AN là tiếp tuyến của đường tròn (O)
2. vẽ đường kính ND. chứng minh MD // AO
3.Xác định vị trí điểm A để tam giác AMN đều
cắt tiếp tuyến tại M của đường tròn tại điểm A.
mình ghi thiếu
Đúng 0
Bình luận (0)
Cho đường tròn (O;R), dây MN khác đường kính. Hai tiếp tuyến của đường tròn (O;R) tại M và N cắt nhau tại K. Kẻ đường kính NI, kẻ MH vuông góc với NI tại H. a) chứng minh OK vuông góc với ON b) chứng minh ON là phân giác góc HMK c) gọi Q là giao điểm của KI và MH. Chứng minh QH = QM
Đề bài sai nhiều quá, em kiểm tra lại câu a là ON hay MN, và câu b là ON hay MN?
Đúng 0
Bình luận (1)
a.
Ta có: \(KM=KN\) (t/c hai tiếp tuyến cắt nhau)
\(OM=ON=R\)
\(\Rightarrow OK\) là trung trực của MN, hay \(OK\perp MN\)
b.
Có \(\widehat{KMN}=\widehat{KNM}\) (do \(\Delta KMN\) cân tại K)
\(\widehat{KNM}=\widehat{HMN}\) (cùng phụ \(\widehat{HNM}\))
\(\Rightarrow\widehat{KMN}=\widehat{HMN}\)
\(\Rightarrow MN\) là phân giác \(\widehat{HMK}\)
c.
Kéo dài IM và NK cắt nhau tại A
Theo câu ta có \(OK\perp MN\Rightarrow OK||IA\) (cùng vuông góc MN)
Mà O là trung điểm IN \(\Rightarrow K\) là trung điểm AN
Hay \(KA=KN\) (1)
Do \(MH||AN\) (cùng vuông góc IN), áp dụng định lý Talet trong tam giác KIN:
\(\dfrac{IQ}{IK}=\dfrac{QH}{KN}\) (2)
Áp dụng định lý Talet trong tam giác AIK:
\(\dfrac{IQ}{IK}=\dfrac{QM}{KA}\) (3)
(1);(2);(3) \(\Rightarrow QH=QM\)
Đúng 0
Bình luận (0)
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC AMa) Chứng minh AB BCb) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyếnMC với đường tròn (C là tiếp điểm).a) Chứng minh OM // BCb) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hànhc) Chứng minh COMN là hình thang cân3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tu...
Đọc tiếp
1. Cho đường tròn (O), đường kính AB, dây AM. Kéo dài AM một đoạn MC = AM
a) Chứng minh AB = BC
b) Gọi N là trung điểm BC. Chứng minh tứ giác BOMN là hình thoi.
2. Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).
a) Chứng minh OM // BC
b) Từ O vẽ đường thẳng vuông góc AB cắt BC tại N. Chứng minh BOMN là hình bình hành
c) Chứng minh COMN là hình thang cân
3.Cho đường tròn (O), đường kính AB, tiếp tuyến Ax. Trên Ax lấy điểm M, vẽ tiếp tuyến
MC với đường tròn (C là tiếp điểm).Kẻ CH vuông góc với AB tại H
a) Chứng minh CA là phân giác góc HCM
b) Kẻ CH vuông góc Ax tại K, gọi I là giao điểm của AC và HK. Chứng minh tam giác AIO vuông
c) Chứng minh 3 điểm M, I, O thẳng hàng
Mọi người ơi giúp e vsssssssssssssss.........E hỏi mà hong ai chỉ T.T
ko làm mà muốn ăn thì chỉ có ăn cứt ăn đầu buồi nhá!
Bài 1:
a,
OM là đường trung bình của tam giác BAC => OM = 1/2*BC
OM = 1/2*AB
=> AB=BC (đpcm).
b,
Tam giác ABC đều => BC = 2*r(O)
MN là đường trung bình của tam giác ABC => MN = 1/2*AB = r(O) = OM = OB =BN => BOMN là hình thoi.